Cours maths 3ème
Agrandissement et réduction
L'objectif est ici de travailler sur les agrandissements et les réductions ainsi que leurs effets sur les longueurs, les aires de figures et les volumes de solides.
Agrandissement et réduction : définition
Définition :
Multiplier toutes les dimensions d’une figure ou d’un solide (longueurs des côtés, des arêtes, rayons) par un nombre k, c’est en faire :
●
- Un agrandissement si k > 1
●
- Un agrandissement si k > 1
Les mesures des angles de la figure sont inchangés.
Exemple d'agrandissement ou de réduction
On considère le plan d’un appartement réalisé à l’échelle 1/ 200 :
On donne :
AB = 6,5 cm et
AD = 2,5 cm.
Quelles sont les dimensions réelles de cet appartement ?
Le plan est réalisé à l’échelle 1/200 signifie que :
● Le plan est une réduction de l’appartement de coefficient 1/200 ou
● L’appartement est un agrandissement du plan de coefficient 200.
6,5 × 200 = 1300 cm = 13 m et 2,5 × 200 = 500 cm = 5 m
Les dimensions réelles de cet appartement sont 13 mètres et 5 mètres.
Activité : agrandissement d'un cube
On considère un cube C1 d’arête 2 cm. 
1) Calculer l’aire d’une face et le volume de ce cube.
Aire d’une face : A = 2² = 4 cm²
Volume du cube : V = 23 = 8 cm3 .
2) On multiplie la longueur de toute les arêtes par 3 on obtient le cube C2.
a) Quelle est la longueur des arêtes du cube C2 ?
b) ) Calculer l’aire de chaque face du cube C2 puis le volume de ce cube.
a) Les arêtes du cube C2 mesurent 2 × 3 = 6 cm.
b) A = 6² = 36 cm².
L’aire de chaque face du cube C2 est 36 cm².
V = 63 = 216 cm3 .
Le volume du cube C2 est 216 cm3.
3) a) Par quel nombre l’aire de chaque face du cube C1 a-t-elle été multipliée pour obtenir l’aire de chaque face du cube C2 ?
On divise l’aire d’une face du cube C2 par l’aire d’une face du cube C1 :
36 ÷ 4 = 9 = 3²
b) Par quel nombre le volume du cube C1 a-t-il été multiplié pour obtenir le volume du cube C2 ?
On divise le volume du cube C2 par le volume du cube C1 :
216 ÷ 8 = 27 = 33
Propriétés des agrandissements et réductions sur les aires et volumes
Propriétés :
Quand on agrandit, ou on réduit une figure, si les dimensions (ou longueurs) sont multipliées par k, alors :
- Les aires sont multipliées par k²
- Les volumes sont multipliés par k3.
Exemples
Exemple 1 :
Un terrain d’aire A = 900 m² est représenté sur un plan à l’échelle 1/2000.
Quelle est l’aire du terrain sur le plan ?
A’ = 900 × (1 / 2 000)² = 900 × (1 / 4 000 000 )= 0, 000 225 m² = 2,25 cm².
Donc, sur le plan, l’aire du terrain est 2,25 cm².
Exemple 2 :
Un pavé a un volume V de 125 cm3. Ses dimensions sont multipliées par 2.
Quel est le volume du pavé agrandit ?
V’ = 125 × 23 = 125 × 8 = 1 000 cm3.
Le volume du pavé agrandit est 1 000 cm3.
Section d'une pyramide ou d'un cône de révolution
La section d’une pyramide ou d’un cône de révolution par un plan parallèle à la base est une réduction de la base.
La section d’une pyramide ou d’un cône de révolution par un plan parallèle à la base est une réduction de la base.
Exemple : pyramide
Exemple :
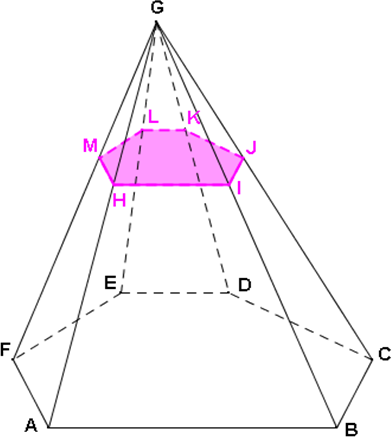
Le plan est parallèle à la base ABCDEF donc :
La section HIJKLM est une réduction de l’hexagone ABCDEF.
Le coefficient de réduction est :
Exemple : cône de révolution
Exemple :
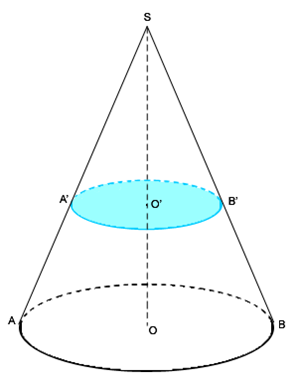
Le plan est parallèle à la base donc :
La section est un cercle.
Ce cercle est une réduction de la base du cône.
Le coefficient de réduction est :
