Espace Client
Espace Client
01 75 85 03 55
01 75 85 03 55 Nous contacter

Cours de maths à partir de 9.90 €/heure

Testez maintenant

Cours maths terminale S - Sommaire général

1. Programme obligatoire

Analyse

Probabilité

Géométrie

2. Programme de spécialité

Arithmétique

Géométrie plane

 

Cours maths terminale S - Sommaire détaillé

 

Programme obligatoire

Analyse

Suites : généralités, suites arithmétiques, suites géométriques

Ce module revient sur tout le programme de première concernant les suites.
Les différents types de suites, la monotonie, la convergence, le tracé des termes d’une suite définie par récurrence, toutes ces notions sont revues avec un seul objectif : développer des outils pratiques afin de faciliter leur manipulation.

Les suites arithmétiques et géométriques, ainsi que l’ensemble de leurs propriétés sont également revues dans le détail, avec un certain nombre de conseils pour éviter les erreurs classiques.

Remarque : seuls les cas de convergence d’une suite définie par une fonction, d’une suite géométrique et d’une suite définie par récurrence sont vus dans ce module.

Suites : raisonnement par récurrence

Dans ce module est introduit un des grands principes de raisonnement en mathématiques : le principe de raisonnement par récurrence.

Ce grand principe expliqué et illustré dans le cas général est ensuite appliqué aux suites.

On apprend alors à l’utiliser et à le rédiger pour démontrer les propriétés d’une suite, propriétés qui ont pu être conjecturées d’après l’étude des premiers termes.

Des exemples d’application sont donnés : démonstration de l’expression du terme général d’une suite, démonstration qu’une suite est bornée.

On élargit ensuite son application à toute formule ou propriétés dépendant d’un entier naturel  n.

Suites : convergence, divergence

Dans ce module consacré à l’étude de la convergence d’une suite, on commence par redéfinir rigoureusement la notion de limite finie d’une suite.

Sont ensuite exposés les outils qui permettent de montrer la convergence d’une suite que sont les théorèmes de convergence monotone et le théorème des gendarmes.

Le même travail est fait pour une limite infinie, la définition étant suivie des théorèmes de divergence monotone et des théorèmes de comparaison.

Le cours se termine par la révision et la démonstration des résultats de convergence précédemment admis dans le premier module sur les suites, à savoir : les cas de convergence d’une suite définie par une fonction, d’une suite géométrique et d’une suite définie par récurrence.

Suites : suites adjacentes

Ce module est consacré à l’étude des suites dites adjacentes.

A la définition de cette notion succède le théorème de convergence de telles suites.

La démonstration de ce théorème pouvant faire l’objet d’un R.O.C, elle est abordée sous la forme d’un exercice comportant plusieurs étapes.

Fonctions : limites

L’objectif de ce module est tout d’abord de faire le point sur la notion de limite d’une fonction, notion découverte en première S.

La partie cours revient sur les définitions de limites finies ou infinies en un point ou en l’infini. Propriétés algébriques et règles calculatoires sont rappelées et les nouveaux outils que sont les théorèmes de comparaison sont introduits.

D’un point de vue graphique, les notions d’asymptote et de positions relatives sont revues dans un cadre plus général, à la fois théorique et pratique.

Fonctions : continuité

Dans ce module, introduction d’une nouvelle notion qu’est la continuité d’une fonction en un point.

En repartant de la définition et de l’illustration graphique d’une limite finie en un point, cette nouvelle notion est abordée tant d’un point de vue graphique que théorique.

Couplée à l’apparition de nouvelles fonctions, définies « par morceaux », la continuité va nous obliger à nous familiariser avec l’étude des limites à gauche et à droite en un point.

La continuité sur un intervalle est ensuite définie et avec elle sont exposées les fonctions de référence et les règles qui permettent de les utiliser.

La partie cours se termine avec le cas des fonctions composées.

Fonctions : dérivabilité, tangente, fonction dérivée

Dans ce module, retour sur la notion de nombre dérivé vue en première.

La classe de terminale s’attardant plus longuement sur le problème de la dérivabilité d’une fonction en un point, les différents cas possibles sont étudiés et à cette étude est couplée celle de la tangente en un point, aspect graphique de la question.

Le lien entre continuité et dérivabilité en un point est également étudié.

Après une partie pratique consacrée à la lecture graphique du nombre dérivé et à la recherche d’équations de tangentes, sans utiliser de formule, la notion de dérivabilité en un point est étendue à la dérivabilité sur un intervalle.

Les fonctions de référence sont introduites ainsi que les règles qui permettent de les utiliser.

On définit alors la notion de fonction dérivée sur un intervalle.

Les formules de dérivation et propriétés algébriques sont révisées.

Le lien entre variations d’une fonction et signe de la dérivée est rappelé et une mise au pont claire est faite sur la différence entre une fonction monotone et une fonction strictement monotone.

Fonctions : théorème des valeurs intermédiaires, bijection

Ce module est consacré aux propriétés liées à la continuité d’une fonction sur un intervalle.

Une mise au point est tout d’abord faite sur la notion d’intervalle et vient ensuite un des grands théorèmes de l’analyse : le théorème des valeurs intermédiaires, suivi de son corollaire.

On étudie les conséquences de ce théorème sur l’image d’un intervalle par une fonction continue, puis on définit la notion de bijection.

S’appuyant sur cette notion, une autre version du corollaire du théorème des valeurs intermédiaires est donnée, appelée : théorème de la bijection.

Les applications de ces théorèmes sont ensuite étudiées et illustrées : existence d’une fonction réciproque, existence et dénombrement des solutions d’une équation, encadrement des solutions d’une équation et déduction du signe d’une fonction.

Primitives : définition, techniques de calcul

Dans ce module est introduite la notion de primitive d’une fonction sur un intervalle.

On commence par définir cette notion puis par montrer qu’une fonction admet une infinité de primitives différant seulement d’une constante.

On apprend alors à rédiger la recherche de la seule primitive vérifiant une condition initiale donnée.

La continuité d’une fonction sur un intervalle étant une condition suffisante à l’existence d’une primitive sur cet intervalle, un rappel est fait sur l’ensemble des théorèmes liés à la notion de continuité.

Les propriétés algébriques des primitives sont démontrées et énoncées dans l’optique de leur utilisation lors des futurs calculs.

Enfin, une technique de calcul des primitives, utilisant ces propriétés, est exposée sur plusieurs exemples.

Cette technique s’appuie exclusivement sur les formules de dérivation et ne nécessite l’apprentissage d’aucune nouvelle formule.

Fonction exponentielle : définition, propriétés, notation puissance, équations, inéquations

Dans ce module est introduite la fonction exponentielle, en tant que seule fonction ayant pour dérivée elle-même et prenant la valeur 1 en 0.

Sa continuité, sa dérivabilité, son signe sont étudiés et un premier bilan pratique, permettant de manipuler la fonction est établi.

On s’intéresse ensuite aux propriétés algébriques de la fonction exponentielle.

Après avoir démontré que la fonction exponentielle réalise une bijection, sa fonction réciproque, la fonction logarithme népérien est introduite.

Cette fonction n’est pas étudiée ici et seul le fait que, grâce à elle, tout nombre strictement positif possède une écriture exponentielle est à retenir.

Ceci afin de pouvoir résoudre équations et inéquations.

La partie cours se termine par l’introduction du nombre e qui nous permet dès lors d’adopter une notation puissance pour la fonction exponentielle.

Les propriétés algébriques sont alors revues sous ce nouveau jour, permettant de réaliser qu’elles ne sont rien d’autre que les propriétés d’une puissance.

Fonction exponentielle : étude, limites, dérivées

Après un bref rappel des résultats vus dans le module de définition de la fonction exponentielle, nous menons l’étude approfondie de cette nouvelle fonction.

Nous voyons ses limites aux bornes, dressons sont tableau complet de variations et traçons sa courbe. Nous intéressant au passage à son asymptote et à deux de ses tangentes.

Une étude de l’exponentielle est ensuite menée au voisinage de 0, ce qui nous fournit un nouveau résultat de limite et une approximation affine.

Nous comparons ensuite les croissances de la fonction exponentielle et de la fonction qui à x associe x. Ceci donnant deux résultats de référence concernant  les limites.

Le cours se termine par l’étude de la dérivation des fonctions composées de type exp(u).

Équations différentielles

Dans ce module très lié à la notion de fonction exponentielle, nous découvrons un nouveau type d’équations : les équations différentielles.

Après une brève explication de ce nouveau concept, nous nous lançons dans l’étude des solutions des équations de type : y’=ay.

Le cas plus général des équations de type : y’=ay+b est ensuite considéré.

L’étude et la démonstration des solutions pour ce type d’équations servant de rédaction référence pour les exercices à venir.

Le cours se termine par la recherche d’une solution particulière pour une équation, une condition initiale étant fixée.

Fonctions logarithmes : définition, propriétés, équations, inéquations

Il existe plusieurs façons d’introduire la notion de fonction logarithme népérien. Dans ce module, nous choisissons de la définir en tant que fonction réciproque de la fonction exponentielle.

Après un bref rappel sur la fonction exponentielle, la fonction logarithme népérien est donc définie. A partir de cette définition, des propriétés sont étudiées, des remarques sont faites et des cas particuliers sont examinés afin de familiariser l’élève avec cette nouvelle fonction. Manipuler une fonction réciproque n’étant pas forcément quelque chose de très intuitif, il est important dans un premier temps de bien comprendre le lien entre exponentielle et logarithme népérien.

Vient ensuite un bilan pratique de tout ce qui a été constaté. L’accent étant mis sur la possibilité d’écrire maintenant certains réels sous deux formes : la forme exponentielle et la forme logarithmique. Ceci servant à résoudre équations et inéquations.

Les propriétés algébriques du logarithme népérien sont ensuite déduites de celles de l’exponentielle.

Il est prouvé que le logarithme népérien est une bijection et qu’il est strictement croissant, ce qui nous permet de mettre au point des techniques de résolution des équations et inéquations contenant un logarithme.

Il est alors temps de montrer l’équivalence avec l’autre façon d’introduire la notion de logarithme népérien, à savoir en tant qu’unique primitive de la fonction inverse s’annulant en 1.

Le cours se termine enfin par l’étude générale des fonctions logarithmes, appelées aussi fonctions logarithmes de base a.

Le logarithme de base 10, noté Log, très utile en chimie est vue plus en détail et une application pratique en est donnée.

Fonctions logarithmes : étude, limites, dérivées

Après un bref rappel des résultats vus dans le module de définition des fonctions logarithmes, nous menons l’étude approfondie de la fonction logarithme népérien.

Nous voyons ses limites aux bornes, dressons sont tableau complet de variations et étudions son signe.

Nous traçons alors sa courbe, nous intéressant au passage à son asymptote et à deux de ses tangentes. Un constat est alors fait sur la symétrie des courbes des fonctions exponentielle et logarithme népérien, fonctions réciproques.

Par l’étude du nombre dérivé en 1, nous obtenons un nouveau résultat de limite et une approximation affine de la fonction x donne ln(1+x) au voisinage de 0.

Nous comparons ensuite les croissances de la fonction logarithme népérien et de la fonction qui à x associe x. Ceci donnant deux résultats de référence concernant  les limites.

Le cours se termine par l’étude de la dérivation des fonctions composées de type ln(u).

Fonctions puissances

Ce module commence par l’étude des croissances comparées des fonctions exponentielle, logarithme et x puissance n.

Ces résultats généralisent les résultats déjà vus pour la fonction identité, qui à x associe x.

Nous généralisons ensuite la notion de puissance, connus depuis toujours pour les exposants entiers, à tout exposant réel. Passant alors en revue les propriétés algébriques d’une puissance, également valables pour ce nouveau type d’exposant.

S’appuyant sur cette définition, les fonctions puissances et les fonctions exponentielles de base a sont alors définies.

Une étude de la fonction exponentielle de base a est alors réalisée, ses limites, variations et sa représentation étant étudiées, en fonction de a.

La notion de fonction racine n-ième est ensuite introduite et le lien est fait avec les fonctions puissances ayant pour exposant 1 sur n.

L’étude générale de ce nouveau type de fonction clôture la partie cours.

Primitives : logarithme, exponentielle

Ce module débute par de rapides rappels sur ce qui a été vu dans le premier module concernant les primitives.

On revoit dans un premier temps la définition de la notion de primitive, le lien entre deux primitives d’une même fonction et l’unicité de la primitive vérifiant une condition initiale.

Ce premier rappel se terminant par un point sur la rédaction à adopter dans la recherche d’une primitive.

Les conditions d’existence d’une primitive sur un intervalle et les propriétés algébriques, utiles aux calculs, sont énoncées.

Vient ensuite une série d’exemples pratiques expliquant la stratégie à adopter afin de passer maître dans l’art de calculer des primitives, sans apprendre la moindre nouvelle formule !

Cette stratégie repose sur la maîtrise des formules de dérivations et sur les 3 propriétés algébriques énoncées plus haut.

Une série d’exemples est en particulier consacrée à la recherche de primitives d’une fonction exprimée sous la forme d’un rapport.

C’est pour cette raison qu’il est obligatoire d’avoir d’abord vu le module sur les fonctions logarithmes.

La partie cours se termine par la recherche de primitives de fonctions faisant intervenir l’exponentielle.

Intégration : définition, lien avec les primitives.

Dans ce module est introduite la notion d’intégrale d’une fonction continue sur un intervalle.

Le cours commence par une mise au point sur la notion d’unité d’aire.

Une illustration graphique du recouvrement de la surface située sous une courbe par des rectangles de faible épaisseur est ensuite donnée afin d’aider à appréhender cette nouvelle notion.

On définit alors l’intégrale d’une fonction, continue, positive sur l’intervalle [ a ; b ] comme étant, en unités d’aire, l’aire de la partie du plan située entre la courbe de f, l’axe des abscisses et les droites d’équations x=a et x=b.

Cette définition est ensuite étendue aux fonctions continues négatives puis à tout type de fonction continue. Des exemples sont fournis.

Vient alors le lien entre intégrale et primitive qui va permettre le calcul des intégrales : le théorème affirmant que la primitive de f s’annulant en a est l’intégrale de a à x de f(t)dt est énoncé mais non démontré.

On en déduit alors la méthode de calcul d’une intégrale à l’aide d’une primitive quelconque.

Pour finir, les propriétés algébriques de l’intégrale sont données.

Il s’agit des propriétés de linéarité et de la relation de Chasles.

Intégration : intégration par parties, intégration et ordre.

Ce deuxième module traitant de la notion d’intégration commence par des rappels.

Définition géométrique de l’intégrale d’une fonction continue sur un intervalle, propriétés algébriques de l’intégrale et méthode de calcul à l’aide d’une primitive sont revues.

Viennent ensuite les théorèmes concernant ordre et intégration.

En partant de la positivité de l’intégrale d’une fonction positive, on déduit d’autres propriétés sur l’ordre, dont la propriété d’inégalité de la moyenne.

Le cours se termine par l ‘exposition de la méthode d’intégration par parties, permettant de calculer l’intégrale d’une fonction produit.

Cette méthode est à la fois démontrée et illustrée par un exemple pratique.

L’accent étant mis sur la rédaction et sur les erreurs de calcul à éviter.

Intégration : valeur moyenne, volumes.

Ce dernier module traitant de la notion d’intégration commence par des rappels concernant les propriétés, définitions et méthodes vues dans les deux autres modules.

Vient ensuite la définition de la valeur moyenne d’une fonction continue sur un intervalle.

Une illustration géométrique en est donnée afin de donner du sens à cette valeur.

On s’intéresse ensuite à la façon de calculer l’aire de la partie comprise entre les courbes de deux fonctions continues sur un intervalle.

La fin du cours détaille de façon pratique et imagée la technique permettant de calculer le volume d’un solide de révolution, solide engendré par la rotation d’une courbe autour d’un axe.

Au delà de la formule trouvée, c’est ici la méthode qui est privilégiée.

 

Probabilité

Probabilités : dénombrement, formule du binôme

Ce module est consacré à la définition et au dénombrement des objets pouvant être le résultat d’une expérience aléatoire.

En prenant pour exemple différentes expériences aléatoires, les objets que sont les p-listes, les arrangements, les permutations et les combinaisons sont dans un premier temps définis.

Puis on apprend à dénombrer les arrangements à l’aide d’un arbre de choix ou à l’aide de cases. Une formule générale en est déduite puis appliquée au cas particulier d’arrangements que sont les permutations. On définit alors la notion de factorielle. Dans la foulée, on apprend à également dénombrer les p-listes.

Le lien est ensuite fait entre le nombre d’arrangements et le nombre de combinaisons des éléments d’un même ensemble. La formule du nombre de combinaisons de p éléments d’un ensemble à n éléments en est déduite.

Ce nombre appelé : « p parmi n » est l’objet d’étude de la fin du cours.

On apprend à le calculer de façon pratique puis ses diverses propriétés sont étudiées, notamment à l’aide du triangle de Pascal.

Le cours se termine par la formule du binôme de Newton.

Probabilités : événements, probabilités, variable aléatoire

A partir d’un exemple concret d’expérience aléatoire, les notions d’issue, d’univers et d’événement sont tout d’abord définies.

Le vocabulaire ensembliste lié à la manipulation des événements est révisé.

Les notions de réunion et d’intersection sont revues, ainsi que le calcul de leur cardinal. Evénement contraire et événements incompatibles sont au passage définis. Un point est également fait sur la notion de partition d’un ensemble.

La notion de probabilité est définie dans le cas général puis dans le cas d’un univers équiprobable. Ses propriétés sont énumérées et démontrées dans le cas de l’équiprobabilité.

Le module se termine par la définition de la notion de variable aléatoire.

Deux exemples concrets de variables aléatoires sont tirés d’une même d’expérience aléatoire. On apprend ensuite de façon pratique à établir la loi de probabilité d’une variable aléatoire. L’étude des paramètres liés à toute loi que sont l’espérance, la variance et l’écart type vient clore la partie cours.

Probabilités : probabilités conditionnelles, expériences successives

On commence dans ce module par définir la notion d’arbre pondéré, à partir d’un exemple simple d’expérience aléatoire.

La répétition de cette expérience de façon indépendante permet ensuite de dresser un arbre pondéré composé.

Après avoir fait le lien entre parcours sur l’arbre et événements, on apprend à remplir un tel arbre et à calculer à l’aide de ce nouvel outil.

La loi des probabilités totales est énoncée puis illustrée à l’aide du calcul sur un arbre pondéré.

Au travers de l’enchaînement d’expériences non indépendantes, la notion de probabilité conditionnelle est ensuite introduite.

Un arbre pondéré de référence est établi, permettant de retenir l’ensemble des formules liées à cette nouvelle notion.

La définition d’événements indépendants et de variables aléatoires indépendantes vient clore la partie cours.

Probabilités : loi binomiale, adéquation à une loi équirépartie

Ce module commence par la définition d’une épreuve de Bernouilli.

Deux exemples d’expériences aléatoires sont ramenés à une schématisation du type Bernouilli grâce à la définition des événements succès et échec.

Une épreuve de Bernouilli de référence est ensuite répétée, définissant ainsi une expérience de Bernouilli.

On apprend alors à calculer les probabilités des événements liés à une telle expérience, en utilisant son arbre pondéré, appelé « schéma de Bernouilli ».

La variable aléatoire dénombrant les succès lors d’une telle expérience est introduite et la loi qu’elle suit est établie.

Le type de loi suivi par cette variable est défini de façon plus générale, sous l’appellation de loi binomiale. Espérance et variance pour une telle loi sont calculées et des exemples de son utilisation sont donnés.

La deuxième partie du cours est consacrée à la mise au point d’un test permettant par exemple de savoir si un dé est pipé.

Ce test comparant résultats statistiques observés et résultats statistiques de référence est appelé test d’adéquation à une loi équirépartie.

Probabilités : lois continues.

Ce module qui clôt le chapitre des probabilités s’intéresse aux lois continues de probabilités.

Le cours commence par une explication sur la différence entre variable aléatoire discrète et variable aléatoire continue.

Au passage, les résultats sur la loi binomiale, qui est une loi discrète, sont rappelés.

On définit ensuite la notion de loi continue comme intégrale d’une fonction appelée densité de probabilité.

Les conditions pour qu’une fonction f soit une densité de probabilité sont détaillées et démontrées.

On étudie alors les résultats généraux liés aux lois ainsi définies : propriétés algébriques, espérance mathématique, techniques de calcul, probabilité de l’événement contraire.

Un exemple de fonction densité est donné ainsi qu’une illustration graphique de la loi continue qu’elle engendre.

On s’intéresse ensuite aux deux cas particuliers de lois continues que sont la loi uniforme et la loi exponentielle.

Pour chacune, les résultats calculatoires qui leurs sont propres sont donnés et démontrés.

Tour en sachant, cependant, que ces résultats sont plus à savoir redémontrer qu’à apprendre.

Le cours se termine par l’explication du lien entre loi exponentielle et loi de durée de vie sans vieillissement.

 

Géométrie

Nombres complexes : introduction, forme algébrique.

Dans ce module, introduction algébrique et manipulation de nouveaux nombres : les nombres complexes.

Après un bref rappel sur la construction de l’ensemble des nombres réels, un premier nombre non réel est défini : i.
A partir de lui, tout un ensemble de nouveaux nombres est créé : l’ensemble des nombres imaginaires purs, nombres dont les propriétés sont ensuite étudiées.
En ajoutant un nombre réel non nul et un nombre imaginaire non nul, un ensemble plus large, contenant réels et imaginaires purs est introduit : l’ensemble des nombres complexes.
L’écriture de ces nombres sous forme algébrique est alors définie et la caractérisation des réels et imaginaires purs écrits sous cette forme est étudiée.
De nombreux exemples d’opérations sont ensuite détaillés pour apprendre à calculer de façon simple et organisée dans ce nouvel ensemble.
Le cas de la division fait l’objet d’une étude particulière et amène à la création de la notion de conjugué d’un nombre complexe. Les propriétés de cette nouvelle notion sont étudiées et on apprend à caractériser réels et imaginaires purs à l’aide du conjugué.

Nombres complexes : équations, représentation dans le plan.

Dans ce module, étude de la résolution d’équations dans l’ensemble des complexes et de la représentation des nombres complexes dans le plan.

Après une étude pratique des équations du premier degré dans 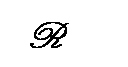, et des équations faisant intervenir le nombre conjugué, la partie cours s’intéresse aux équations du second degré à coefficients réels dans .
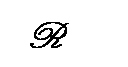L’utilisation du discriminant, vue en première, est étendue aux nombres complexes et un théorème, simple, valable sur les réels et les complexes est découvert puis énoncé.
La suite du cours fait le lien entre géométrie plane et nombres complexes de façon progressive et originale.
Le lien est d’abord fait avec les vecteurs, définition de l’affixe d’un vecteur et étude de ses propriétés, puis définition de l’affixe d’un point et lien avec tout ce qui a été vu pour l’affixe d’un vecteur. La notion de plan complexe est alors définie.
Au passage, la configuration de référence liée au conjugué est étudiée et affixe du milieu et du barycentre sont vues.

Nombres complexes : forme trigonométrique.

Dans ce module, définition du module, de l’argument et de la forme trigonométrique d’un nombre complexe.
Comme dans le module faisant le lien entre nombres complexes et géométrie plane, les définitions du module et de l’argument sont d’abord introduites en s’appuyant sur les vecteurs. Ceci garantit que l’élève sera capable d’envisager la résolution d’exercices sortant des sentiers battus et capable de réaliser la démonstration des ROCs les plus fins.
La partie cours commence donc par l’étude du module d’un nombre complexe.
La définition en est donnée par l’intermédiaire de la norme du vecteur image, son calcul pratique en est déduit puis ses propriétés étudiées.
Une étude identique est menée sur l’argument d’un nombre complexe.
De nombreux exemples sont étudiés et amènent à la caractérisation des réels et des imaginaires purs à l’aide de l’argument.
Le lien est ensuite fait entre coordonnées polaires d’un point et module et argument de son affixe, cette relation menant à la définition de la forme trigonométrique d’un nombre complexe.
Unicité de l’écriture sous forme trigonométrique et passage de la forme algébrique à la forme trigonométrique sont étudiés.
Le tracé de l’image d’un nombre complexe défini sous forme trigonométrique et les configurations de références sont également abordés.

Nombres complexes : forme exponentielle.

Dans ce module, définition, manipulation et étude de l’écriture d’un nombre complexe sous forme exponentielle.
Dans un premier temps le cours est consacré à l’étude des nombres complexes de module 1. L’écriture à l’aide de l’exponentielle de ces nombres est introduite et des exemples de référence sont étudiés. Les propriétés liées à l’exponentielle sont exposées et la configuration de référence liant un nombre de module 1, son conjugué et son opposé est étudiée.
L’écriture exponentielle est enfin généralisée à tout nombre complexe de module non nul. L’unicité de cette écriture est prouvée puis quelques exercices de base illustrant le côté pratique de cette écriture sont résolus.
Le cours se termine par les formules d’Euler puis par l’étude de l’équation paramétrique d’un cercle.

Nombres complexes : transformations du plan complexe.

Dans ce module sont étudiées certaines transformations du plan complexe, du point de vue de leur écriture complexe et du point de vue de leurs propriétés géométriques.
Dans un premier temps, le cours revient sur la définition d’une transformation dans le plan puis fait le tour de transformations rencontrées dans la scolarité jusqu’en classe de terminale.
Vient ensuite l’étude détaillée des translations, des homothéties et des rotations.
Dans chaque cas l’étude se partage en recherche de l’écriture complexe de la transformation, justification calculatoire et graphique de l’écriture, étude de la réciproque et étude des propriétés géométriques de la transformation.
Dans le cas de la rotation, les configurations de référence que sont le triangle rectangle isocèle et le triangle équilatéral sont étudiées.
Un bilan pratique est enfin dressé pour apprendre à identifier les transformations complexes dont l’écriture est du type : z’=az+b.

Produit scalaire et orthogonalité.

Ce module commence par un rappel concernant la définition de l’orthogonalité de deux vecteurs du plan. Notion pouvant être étendue à l’espace.
On définit ensuite l’orthogonalité entre deux droites puis entre un plan et une droite ; cette première partie se terminant par la définition du plan médiateur d’un segment.

Le point est ensuite fait sur les diverses définitions et multiples propriétés du produit scalaire de deux vecteurs, du plan, ou de l’espace.
On y revoit sur des exemples concrets les diverses techniques de calcul : utilisation du projeté, décomposition en vecteurs colinéaires ou orthogonaux, utilisation du cosinus, déduction à partir des normes et enfin expression analytique.
La propriété comme quoi deux vecteurs sont orthogonaux si et seulement si leur produit scalaire est nul est également revue et démontrée.

De l’expression analytique on déduit les formules de calcul de la norme d’un vecteur et de calcul de la distance entre deux points.

La troisième partie du cours s’intéresse à l’équation cartésienne d’une droite du plan.
La notion de vecteur normal à une droite du plan est alors introduite et quelques techniques simples permettant de manipuler ces notions sont exposées.
On définit ensuite la notion de distance d’un point à une droite et la formule de calcul est donnée.
Le cours se termine par les équations cartésiennes du cercle et de la sphère.

Géométrie dans l’espace : équation(s) de plans, position relative par rapport à un plan.

Ce module commence par les différentes façons de définir un plan de l’espace :
définition à partir de 3 points non alignés, définition à partir d’un point et de deux vecteurs non colinéaires et définition à partir d’un point et d’un vecteur normal.

La deuxième définition nous permet d’introduire la représentation paramétrique d’un plan et la troisième définition nous permet d’introduire la notion d’équation cartésienne d’un plan.
On apprend alors à déterminer l’équation cartésienne d’un plan donné de diverses façons.
La notion de demi-espace de frontière, un plan donné, est expliquée et illustrée.
Nous nous penchons ensuite sur les positions relatives de deux plans : plans parallèles, plans sécants et plans orthogonaux.
Des outils simples et pratiques de détermination de la position relative sont donnés.
Nous faisons ensuite de même pour les positions relatives d’une droite et d’un plan puis d’une sphère et d’un plan.
Entre temps, la formule permettant de calculer la distance d’un point à un plan, utile à l’étude de la position de la sphère par rapport au plan, a été donnée.

Géométrie dans l’espace : représentation(s) de droite, positions relatives.

Ce module commence par les différentes façons de définir une droite de l’espace : définition à partir d’un point et d’un vecteur directeur et définition en tant qu’intersection de deux plans non parallèles.

La première définition nous permet d’introduire la notion de représentation paramétrique d’une droite tandis que la deuxième définition permet d’introduire la représentation d’une droite à l’aide d’un système d’équations cartésiennes.

Nous nous intéressons ensuite à la position relative d’une droite par rapport à un plan. Différentes techniques sont alors données pour montrer qu’une droite est strictement parallèle à un plan, contenue dans un plan ou sécante à un plan.

La position relative de deux droites est ensuite étudiées : droites coplanaires
( sécantes ou parallèles ) et droites non coplanaires. Là encore des outils pratiques sont donnés à travers la résolution d’exemples.

Viennent ensuite deux points clés du module : savoir passer pour une droite, d’une représentation par un système à une représentation paramétrique, ainsi que savoir montrer qu’une droite donnée est l’intersection de deux plans. Trois exemples pratiques de questions de type BAC sont donnés et résolus.

Le cours se termine par l’étude exhaustive de l’intersection de 3 plans. Le but étant de trouver leur intersection, qui peut être l’ensemble vide, une droite ou un point.

Géométrie dans l’espace : barycentre, ensemble de points.

Le cours de ce module est un rappel des définitions et propriétés du barycentre dans le but de les appliquer à la résolution de problèmes liés à l’espace.

C’est pourquoi après avoir revu de façon synthétique et pragmatique les différentes propriétés du barycentre, trois exemples d’exercices types sont donnés et résolus.

Sommaires