Cours maths Terminale S

Complexes - transformations

Dans ce module sont étudiées certaines transformations du plan complexe, du point de vue de leur écriture complexe et du point de vue de leurs propriétés géométriques.

 

1/ Application, image, antécédent.

Dans le plan complexe P rapporté à un repère orthonormé :
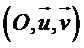
Soit f application définie par :


Selon la nature de f, un point peut ne pas avoir d’image comme il peut ne pas avoir d’antécédent ou bien encore en posséder plusieurs.

Exemples :

1° Si M’ est tel que : Alors le point O n’a pas d’image par f.
Et f est alors simplement définie dans le plan P privé de O.

2° Si M’ est tel que : z' = z² Alors tout point de P a une image par f.
Tout point de P possède également un antécédent mais celui-ci n’est pas forcément unique.
Par exemple, A(-1) possède deux antécédents :B(i) et C(-i).

 

2/ Transformation du plan : définition.

Dans le plan complexe P rapporté à un repère orthonormé :
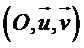
Soit f application définie par :


Si f possède les deux propriétés suivantes :
1° ) Tout point du plan P a une image.
2° ) Tout point du plan P a un antécédent unique.
Alors f est une bijection du plan dans lui-même et est appelée transformation du plan.

L’image d’une droite est une droite parallèle. L’image du cercle C de centre A et de rayon r, C est le cercle C ’ de centre A’ et de rayon r, avec

Remarque

Une translation qui conserve les distances est appelée isométrie
La démonstration detaillée de toutes ces propriétés est du programme de la Première S.
Mais attention, ces propriétés, elles sont, au programme du BAC et sont souvent méconnues des élèves.

Propriété

1° f admet alors une application réciproque, notée f , qui est elle aussi une transformation du plan.
2° Si A ≠ B alors f(A) ≠ f(B) . Deux points distincts ont des images distinctes.


En effet, on ne peut avoir en même temps :
A et B distincts et f (A)=f (B) car alors A’=f (A) pourrait aussi s’écrire A’=f (B) et aurait deux antécédents distincts A et B par f.
Ce qui est contraire à la propriété 2°.

 

3/ Transformation du plan : catalogue.

Les transformations rencontrées jusqu’en classe de terminale sont les suivantes :

- les translations.
- les homothéties.
- les rotations.
- les symétries axiales, également appelées réflexions.
- les symétries centrales.

Remarque

1) La projection orthogonale n'est pas une transformation du plan car deux points distincts peuvent avoir la même image.

2) Symétrie, homothéties et rotations sont des cas particuliers de transformations appelées similitudes, dont l'étude du cas général est uniquement au programme de spécialité.

Une similitude transforme en un triangle semblable, notion vue en classe de Seconde.

3) l'étude du cas particulier qu'est la symétrie axiale ne fait pas non plus partie de l'enseignement obligatoire.

4) Les symétries centrales sont des cas particuliers d'homothéties et de rotations.

5) On appelle identité, notée Id, la transformation du plan par laquelle tout point du plan a pour lui même. La translation de vecteur nul, toute homothétie de rapport 0 et toute rotation d'angle nul, sont l'identité.

Les transformations que nous allons étudier sont donc :



Pour chaque type de transformation, cette étude consiste à s'interesser aux éléments suivants.
- points invariants et éléments caracteristiques.
Les points invariants sont aussi appélés point fixe.

- influence sur les vecteurs, les distances, les angles, le parallélisme,l'alignement et les figures géométriques.

- écriture complexe.

- transformation réciproque.

 

4/ Translations du plan complexe

Définition

La translation de vecteur est la transformation du plan, noté , qui à tout point M fait correspondre le point M' tel que :

Dans le plan complexe P rapporté à un repère orthonormé:


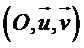
Donc écriture complexe de :

Illustration graphique

Ce résultat est très simple à retrouver et à expliquer graphiquement :

Remarques

1) est l’identité et tous les points du plan sont alors invariants.
2) Si 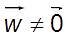, ne possède aucun point invariant.
3) Comme dans la démonstration nous avons procédé par équivalence, nous avons également démontré le résultat réciproque, à savoir :

Si f est une application du plan complexe telle que : z' = z + b
M(z) a pour image M’(z’) avec
alors f est la translation de vecteur d’affixe b.

4) Une translation ne possède qu’un seul élément caractéristique : son vecteur. Autrement dit, elle est entièrement définie ou caractérisée par la donnée d’un vecteur.

5) La transformation réciproque de est : .

Propriétés

D’où :

Les translations conservent :

les distances, le parallélisme, l’alignement et les angles orientés.

Par une translation :
L'image d'une droite est une droite parallèle
L'image du cercle C de centre A et de rayon r , est le cercle C' de centre A' et de rayon r, avec A' = (A)

 

5/ Homothéties du plan complexe

Définition

k étant un réel, non nul.

L’homothétie de centre Ω et de rapport k est la transformation du plan, notée h(Ω,k) ,qui à tout point M fait correspondre le point M’ tel que :

Dans le plan complexe P rapporté à un repère orthonormé :



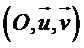
Donc : Ecriture complexe de h(Ω,k)

 

6/ Homothéties du plan complexe : illustration graphique

Commençons par le cas particulier des homothéties de centre O et de rapport k :











Généralisations à toutes les homothéties :

Remarque

1) Quel que soit le point Ω , h(Ω,1) est l’identité et tout point du plan est alors invariant par h.
2) Si k ≠ 1 alors h(Ω,1) admet un seul point invariant : son centre Ω.
3) Quel que soit le point Ω , h(Ω,1) est la symétrie centrale de centre Ω.
4) Comme dans la démonstration nous avons procédé par équivalence, nous avons également démontré le résultat réciproque, à savoir : Soit f est une application du plan complexe telle que :
M(z) a pour image M’(z’) avec z' − ω = k(z - ω).

Si k est un réel non nul alors f est l’homothétie de centre Ω d’affixe ω et de rapport k.
5) Une homothétie possède deux éléments caractéristiques : son centre et son rapport. Elle est donc entièrement définie ou caractérisée par la donnée d’un point et d’un réel.

6) La transformation réciproque de h(Ω,k) est : .

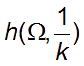Propriétés

D'où
Les homothéties conservent :
le parallélisme, l’alignement et les angles orientés.

Les homothéties multiplient :

Les distances par |k| , les aires par k² .
Et les volumes par |k|³dans l'espace.
h est une isométrie si et seulement si |k| = 1.
Autrement dit, les seules homothéties a être des isométries les symétries centrales et identité.

Par une homothétie :
- L’image d’une droite est une droite parallèle.
- L’image du cercle C de centre A et de rayon r,


est le cercle C ’ de centre A’ et de rayon |k|r , avec A' = h(A)

 

6/ Rotations du plan complexe : définition

Définition

θ étant un angle défini à 2kπ près.

La rotation de centre Ω et d'angle θ est la transformation du plan, notée r(Ω,θ) , qui à tout point M fait correspondre le point M' tel que :
Cet angle n’est pas défini pour M = Ω mais l’égalité de distance suffit pour définir l’image de Ω . En effet : ΩΩ' = ΩΩ = 0
Donc Ω a pour image lui-même.

Dans le plan complexe P rapporté à un repère orthonormé :


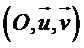
La recherche de l’écriture complexe va être ici plus compliquée que dans les cas précédents. Elle fait d’ailleurs souvent l’objet d’un R.O.C dans les sujets du BAC.





Le nombre complexe ayant pour module 1 et pour argument θ , il s’écrit sous forme exponentielle : 1e^iθ

Dans le plan complexe P rapporté à un repère orthonormé :



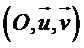
La formule trouvée peut donc être étendue à M = Ω
Ecriture complexe de : r(Ω,θ)

z' − ω = e^iθ(z − ω)   Avec   ω = Z_Ω;

Remarque :

Cette formule résume à elle seule la puissance des nombres complexes, qui permettent de ramener à une simple égalité une configuration très complexe de la géométrie plane.

 

6/ Rotations du plan complexe : illustration graphique

Commençons par le cas particulier des rotations de centre O :

Remarques

1) Quel que soit le point Ω , r(Ω,θ) est l’identité et tout point du plan est alors invariant par r.
2) Si θ ≠ 0 + 2kπ alors r(Ω,θ) admet un seul point invariant : son centre Ω .
3) Quel que soit le point Ω , r(Ω,π) est la symétrie centrale de centre Ω .
4) Comme dans la démonstration nous avons procédé par équivalence, nous avons également démontré le résultat réciproque, à savoir :

Si f est une application du plan complexe telle que :
M(z) a pour image M’(z’) avec
alors f est la rotation de centre Ω d’affixe ωt d’angle θ;
5) Une rotation possède deux éléments caractéristiques : son centre et son angle. Elle est donc entièrement définie ou caractérisée par la donnée d’un point et d’un angle.
6) La transformation réciproque de r(Ω,θ) est : r(Ω,−θ) .

 

6/ Rotations du plan complexe : propriétés

D’où :
Les rotations conservent :
les distances, le parallélisme, l’alignement et les angles orientés.

Par une rotation : Les rotations sont des isométries.
- L’image d’une droite est une droite qui forme avec la droite de départ un angle géométrique égal à la valeur absolue de l’angle orienté de la rotation.
- L’image du cercle C de centre A et de rayon R, est le cercle C ’ de centre A’ et de rayon R, avec A' = r(A) .

 

6/ Rotations du plan complexe : configurations de référence

1) Le triangle rectangle isocèle
ABC triangle rectangle isocèle direct

De même
ABC triangle rectangle isocèle indirect .

2) Le triangle équilatéral
ABC triangle équilatéral direct

De même
triangle équilatéral indirect ABC triangle équilatéral indirect

Utilisation :

Dans un sens, connaissant les affixes des points,pour montrer qu’un triangle est équilatéral ou rectangle isocèle, il suffira de montrer qu’un point est image d’un autre en utilisant l’écriture complexe de la rotation.

Dans l’autre sens, sachant que le triangle est équilatéral ou rectangle isocèle, on utilisera l’écriture complexe de la rotation pour trouver l’affixe manquante.

 

7/ Ecriture complexe : bilan

Soit f application définie par :
Si f =
z' = z + b Avec
Formule très simple à retrouver et rédemontrer.

Si f = h(Ω,k)
Avec : ω = Z_Ω
Formule qui se retrouve immediatement par passage des vecteurs aux affixes

Si f = h(Ω,θ) formule plus difficile à redémontrer et à retrouver mais facile à retenir à partir de l'homothétie

 

8/ Réciproque : démonstration

Considérons maintenant le problème inverse : une écriture complexe nous est donnée et il faut identifier la transformation à laquelle elle correspond.

Soit f application définie par :


Dont l’écriture complexe est du type : z' = az + b avec a ≠ 0.
Une méthode pour identifier une transformation d’après son écriture est de commencer par chercher ses points invariants :


Pour continuer la résolution, il faut diviser par (1-a), ce qui n’est pas possible pour 1-a=0.
D’où l’étude d’un premier cas
1° a = 1 Alors : z' = z + b et f est la translation de vecteur d’affixe b
2° a ≠ 1 Alors : M(z) invariant par f f admet donc un unique point invariant que nous nommerons Ω d’affixe



On retombe alors sur les réciproques vues plus haut, à savoir :

- si a est réel, f est l’homothétie de centre Ω et de rapport a
- si a est de module 1, il peut s’écrire sous la forme e^iθ et f est la rotation de centre Ω et d’angle θ;

 

8/ Réciproque : bilan.

Soit f l'application définie par


Dont l'écriture complexe est du type : z' = az + b avec a ≠ 0

Remarque :

Le cas a non réel de module différent de 1 est étudié dans le programme de spécialité On y étudie en fait le cas général : a nombre complexe quelconque,qui correspond à l’étude des similitudes ( directes ) dont homothéties et rotations sont des cas particuliers.

Les nombres complexes réussissent donc le tour de force de réunir sous une même formule, toutes les transformations ( directes ) du plan.