Cours maths Terminale S

Fonctions - limites

L’objectif de ce module est tout d’abord de faire le point sur la notion de limite d’une fonction; Puis, on verra les définitions de limites finies ou infinies en un point ou en l’infini ; les propriétés algébriques et règles calculatoires sont rappelées et les nouveaux outils que sont les théorèmes de comparaison sont introduits.

 

 

De même :

On dit que f admet comme limite lorsque x tend vers si :
pour tout intervalle du type ] ; A [ il existe un réel a tel que : si x alors
Autrement dit :
« Aussi négatif et grand en valeur absolue que l’on choisisse A, il existe toujours une valeur de x à partir de laquelle, toutes les images sont plus petites que A. »

 

Illustration graphique :

 

Sur le même principe, on définit les limites infinies en
On dit que f admet comme limite lorsque x tend vers si :
pour tout intervalle du type ] A ; [ il existe un réel a tel que : si x
Autrement dit :
"aussi grand que l'on choisisse A, il existe toujours une valeur de X avant laquelle, toutes les images sont plus grandes que A."

 

Remarque :
il est plus parlant de se dire que l’on se déplace des positifs vers les négatifs, et qu’il existe un x à partir duquel toutes les images sont plus grandes que A.

 

Illustration graphique :

De même :
On dit que f admet comme limite lorsque x tend vers si :
pour tout intervalle du type ] ; A [ il existe un réel a tel que : si x

Autrement dit :
" aussi négatif et grand en valeur absolue que l'on choisisse A, il existe toujours une valeur de x avant laquelle, toutes es images sont plus petites que A."

 

 

Au delà des définitions, assez peu utiles pour le BAC, excepté pour de rares R.O.C, une première chose importante à savoir faire est de savoir lire graphiquement une limite.

Pour lire par exemple la limite de f lorsque x tend vers , il faut regarder le comportement de f(x) quand sur l’axe des abscisses on déplace x vers

 

 

Deuxième chose importante à connaître : les limites infinies des fonctions de référence.

Remarque :
Ces limites se démontrent aisément en utilisant la définition et peuvent être retrouvées par lecture graphique.

 

2/ Limite d’une fonction en l’infini : limite finie

Soit f fonction réelle et un nombre réel ( fini )
Définition :

On dit que f admet comme limite lorsque x tend vers si :
pour tout intervalle ] A ; B [ contenant il existe un réel a tel que : si x > a alors
Autrement dit :
« Aussi 'étroit' que l’on choisisse l’intervalle autour de , il existe toujours une valeur de x à partir de laquelle, toutes les images sont dans cet intervalle. »

Notation :

 

Propriété :
* Si f admet une limite finie en alors cette limite est unique.
Le même type de définition existe au voisinage de .

Illustration(s) graphique(s) :

 

 

La courbe tend donc à « se coller » sur la droite horizontale d’équation : y =
Elle peut venir s’y coller, par le dessous,, par le dessus ou en oscillant.

 

* si elle vient se coller par le dessous, :On dit alors que f tend vers par valeurs inférieures et on note :

* si elle vient se coller par le dessus : On dit alors que f tend vers par valeurs supérieures et on note :

* si elle oscille : La droite d’équation : y = est appelée asymptote horizontale à la courbe en

 

On dit alors que la courbe de f admet une asymptote horizontale d’équation : y = au voisinage de

 

Remarque :
par convention, les asymptotes sont tracées en pointillés, ci dessus vue comme une ligne rouge.

 

Cas particulier de la limite nulle
Dans le cas où la limite est nulle, f tend vers 0 par valeurs supérieures signifie que la fonction tend vers 0 en gardant des valeurs positives au voisinage de l’infini.

Dans le cadre d’un calcul de limite faisant par exemple intervenir un quotient,
nous verrons plus loin qu’il est capital de savoir si le dénominateur tend vers 0+-

 

Fonctions de référence

La fonction de référence, étudiée dès la classe de seconde, qui possède une limite finie en l’infini est la fonction inverse : ou 0

Toute fonction constante tend bien entendu également vers un nombre fini en l’infini : si pour tout x : f (x) = b alors :
En particulier, cas important d’un point de vue algébrique :

 

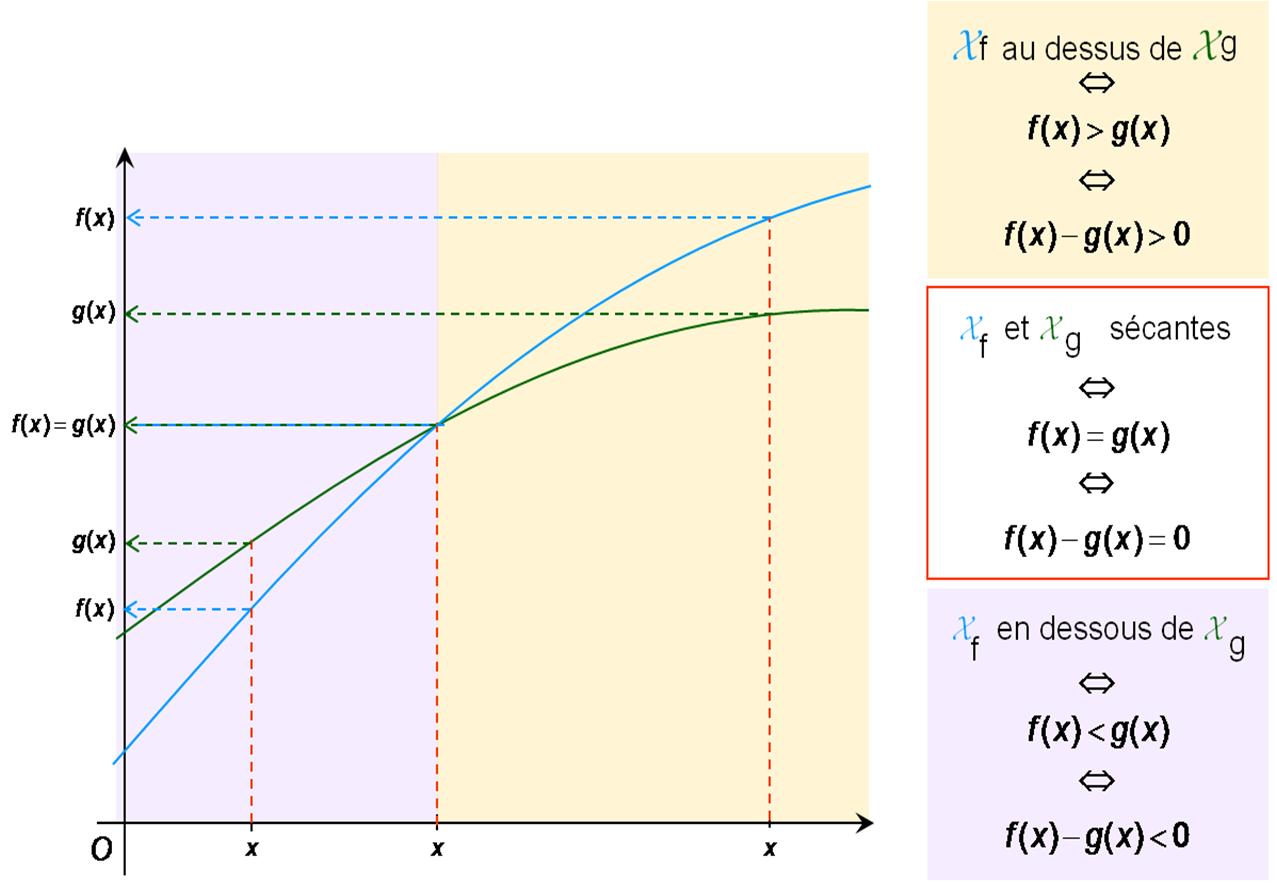
3/ Position relative de deux courbes

Soient deux fonctions réelles f et g et soient leurs courbes Xf et Xg

 

4/ Asymptote à une courbe

Nous allons généraliser la notion d’asymptote vue dans le cas d’une limite finie en l’infini.

Soient deux fonctions réelles f et g et soient leurs courbes Xf et Xg.
On dit que Xg est asymptote à Xf en si Xf vient « se coller » sur Xg quand x tend vers

En résumé
* L’étude du signe de : f(x) - g(x) nous donne la position relative de Xf par rapport à Xg

* L’étude de la limite de : f(x) - g(x) nous dit si Xf admet Xg comme asymptote.

Cas particulier

Si g (x) est du type : g(x) = ax + b
alors la fonction g est affine et sa courbe est la droite (D) d’équation : y : ax + b
* Si a = 0 , l’asymptote est horizontale,, c’est le cas vu plus haut.
* Si a 0 , l’asymptote est dite oblique.

 

5/ Limite d’une fonction en un nombre fini : limite infinie

Soit x0 un nombre réel (fini) et f fonction réelle définie au voisinage de x0

Définition
On dit que f admet comme limite lorsque x tend vers x0 si :
pour tout intervalle du type ] A ; [ il existe un intervalle ] a ; b [ contenant x0 tel que :
Si x ] a ; b [ alors : f (x) ] A ; [

Autrement dit :
« Aussi grand que l’on choisisse A, si les x sont assez proches de x0 alors leurs images sont plus grandes que A. »

Notation


Remarque
une définition équivalente existe pour

 

Illustration graphique

 

La courbe de f tend donc à « se coller » sur la droite verticale d’équation : x = x0 que l’on qualifie par conséquent d’asymptote.

 

 

On dit alors que la courbe de f admet une asymptote verticale d’équation : x = x0

Cette situation se produit souvent quand f n’est pas définie en x0

Remarque :
Pour une limite en un nombre fini, on parle également de limite à droite et limite à gauche.
Encore appelées : limite par valeurs inférieures et valeurs supérieures.

par exemple :
f admet comme limite à droite en x0
Ou encore f admet comme limite par valeurs supérieures en x0

si et seulement si :
aussi grand que l’on choisisse A, si x est assez proche de x0 tout en lui restant supérieur alors son image est plus grande que A.

 

Exemple de référence et notation

On a en général besoin d’étudier la limite des deux côtés de x0 quand f n’est pas définie en x0 , ou quand la définition de f n’est pas la même des deux côtés de x0

 

6/ Limite d’une fonction en un nombre fini : limite finie

Le cas de la limite finie d’une fonction en un nombre fini déjà vu en Première S fait l’objet d’une étude plus approfondie en Terminale S.

En ce qui nous concerne, cette étude sera faite dans un autre module où est introduite la notion de continuité en un point pour une fonction.

 

7/ Limite d’une fonction composée

Limite d’une fonction composée : a, b et c pouvant prendre des valeurs finies ou infinies :

 

8/ Propriétés algébriques des limites

a pouvant prendre une valeur finie ou infinie 0

 

Mais ces limites pouvant être infinies, pour pouvoir appliquer ces formules, il faut connaître les règles opératoires suivantes :

 

9/ Règles opératoires sur les limites : addition

Addition de limites : a pouvant prendre une valeur finie ou infinie.

 

F.I signifie : Forme Indéterminée

En d’autres termes, la limite de la somme varie selon le cas étudié et l’on ne peut donc pas émettre un théorème recouvrant le cas général.

Preuve que l’on ne peut émettre de théorème dans ce cas.

 

9/ Règles opératoires sur les limites : multiplication

Multiplication de limites :
la règle du signe d’un produit de deux réels s’étend au produit de limites finies ou infinies.
tableau opératoire : a pouvant prendre une valeur finie ou infinie.

Le signe est donné par la règle des signes

 

9/ Règles opératoires sur les limites : division

Division de limites : a pouvant prendre une valeur finie ou infinie.

 

Conseil :
Prendre l’habitude de toujours préciser le signe du 0 quand il est le résultat d’une limite. Cela peut en effet être très utile en particulier s’il y a composition de fonctions.

 

Remarque :
est souvent considéré comme une F.I par les élèves.
Pour se persuader du contraire, il suffit de prendre un nombre « énorme» ( le mieux est de prendre une puissance de 10 ) et de le diviser par un « minuscule ».

 

Par exemple :
= 10+35qui est énorme, donc a priori :

 

Attention !
Cette technique n’a aucune valeur de preuve et est à appliquer avec précaution.

 

10/ Théorèmes de comparaison

Parfois les règles de calcul ne suffisent pas pour déterminer une limite et il faut alors faire appel à des théorèmes de comparaison.

C’est le cas notamment pour des fonctions fabriquées à partir de fonctions trigonométriques, les fonctions trigonométriques n’ayant pas de limite en l’infini.

a pouvant prendre une valeur finie ou infinie :

 

Théorèmes de comparaison pour des limites infinies
Si au voisinage de a, on a : f (x) > g (x) et
alors :
Si au voisinage de a, on a : f (x) g (x) et alors :

 

Théorème de comparaison pour une limite finie : Théorème des gendarmes
Si au voisinage de a, on a :