Cours de maths à partir de 9.90 €/heure
Cours maths Terminale S
Intégration
Dans ce module est introduite la notion d’intégrale d’une fonction continue sur un intervalle. Le cours commence par une mise au point sur la notion d’unité d’aire.
1/ Notion d’unité d’aire, bases avant l'intégration
Définition :
Soit le repère
orthogonal
L’
unité d’aire est l’aire du rectangle OIKJ et se note u.a.
Notion d’unité d’aire
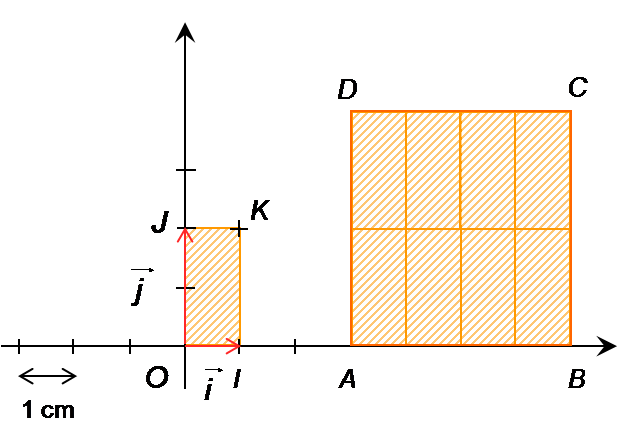
Dans le cas du repère On a alors Aire(ABCD) = 8 u.a.
Ce qui peut être démontré de deux façons :
Aire (ABCD) = 4 x 4 = 16 cm2 D’où : Aire (ABCD) = 16 / 2 = 8 u.a.
Ou de la façon suivante :
si on note u.x l’unité sur les abscisses et u.y celle sur les ordonnées.
Alors : AB = 4 cm = 4 u.x et AD = 4 cm = 2 u.y.
D’où : Aire (ABCD) = 4 u.x x 2 u.y = 8 u.a
Si maintenant on considère par exemple le repère
.png)
On a alors :
D’où Aire(ABCD) = 4 u.a.
2/ Intégration : approche de la notion d’intégrale
Soit f fonction continue sur l’intervalle [ a ; b ]. Et soit X sa représentation dans le repère
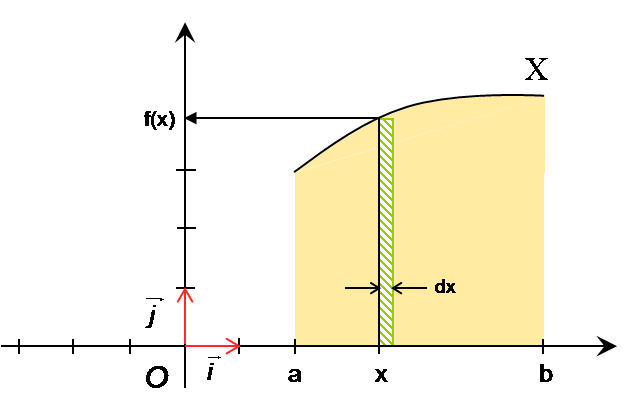
Appelons A, l’aire de la surface orange située sous la courbe et mesurée en unités d’aire.
L’aire du petit rectangle vert est f (x) x dx
La surface orange peut être « quasiment » recouverte par des rectangles de ce type avec x allant de a à b.
Plus l’écart dx sera petit et plus la somme des aires des rectangles sera proche de A.
Autrement dit,
la somme des f(x)dx tend vers A quand dx tend vers 0, pour x allant de a à b.
Cette limite de somme est notée avec un grand s étiré : qui se lit
intégrale..
Les bornes de l’intervalle sont appelées
bornes de l’intégrale et notées :
Cette égalité entre aire et limite de somme se note dans sa globalité : A
3/ Intégration : intégrale d’une fonction continue positive
Définition :
Soit f fonction continue
positive sur un intervalle [ a ; b ] ( avec a < b ).
Et soit X sa représentation dans le repère
L’intégrale de la fonction f sur [ a ; b ] notée est en
unités d’aire, l’aire de la partie du plan limitée par :
Remarques :
1) se lit : « intégrale de a à b de f (x) dx »
2) a et b sont appelées bornes de l’intégrale ou bornes d’intégration.
3) Si les bornes sont égales, l’intégrale est nulle :
4)
x est appelée variable d’intégration, c’est une variable « muette ».
Il s’agit d’une variable qui comme nous le verrons plus tard sert uniquement à réaliser un calcul. C’est pourquoi elle peut être remplacée par une autre lettre.
Remplacement qui s’avèrera obligatoire dans certains cas.
5) Dans les calculs, on note souvent l’intégrale avec un i majuscule : I
6) Si f est la fonction nulle sur [ a ; b ] alors = 0
Exemple :
Soit définie sur R
est , en unités d’aire, l’aire comprise entre C, (Ox), x = 2 et x = 6.
C’est à dire l’aire du trapèze ABCD.
Or :
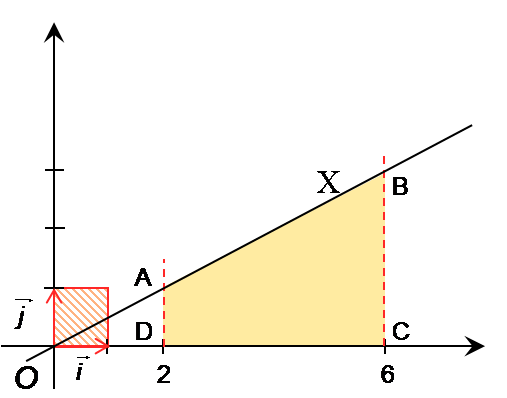
et : 1 u.a. = 1 cm3
donc : = 8
4/ Intégration : intégrale d’une fonction continue négative
Définition :
Soit f fonction continue négative sur un intervalle [ a ; b ] ( avec a < b ). Et soit X sa représentation dans le repère
L’intégrale de la
fonction f sur [ a ; b ] notée
est en unités d’aire, l’opposé de l’aire de la partie du plan limitée par :
5/ Intégration : intégrale d’une fonction continue
Définition :
Soit f fonction continue sur un intervalle [ a ; b ] ( avec a < b ).
Et soit X sa représentation dans le repère
L’intégrale de la fonction f sur [ a ; b ] notée
est en unités d’aire, la différence entre :
les aires situées au dessus de (Ox) et les aires situées en dessous de (Ox).
6/ Intégration : lien entre intégrale et primitive
La notion de primitive est définie et étudiée dans deux modules indépendants.
On apprend entre autre dans ces deux modules à calculer la primitive d’une fonction
sans avoir à retenir la moindre nouvelle formule.
Cette technique s’appuie uniquement sur la maîtrise des formules de dérivation.
Il est donc conseillé d’avoir vu au préalable au moins l’un de ces deux modules
pour comprendre le cours qui va suivre et pour pouvoir aborder la partie exercices.
Théorème :
Soit f fonction continue sur un intervalle I de R.
Et soit a réel, appartenant à I.
La fonction F définie pour tout x de I par :
est l’unique primitive de f sur I qui s’annule en a.
Nous admettrons la démonstration de ce théorème.
Cette démonstration assez théorique utilise le théorème des gendarmes
et les notions de nombre dérivé et de continuité en un point.
On y démontre d’une part que pour tout x de I : F’(x) = f (x).
Autrement dit que F est une primitive de f sur I.
Et d’autre part, comme , F est bien l’unique
primitive de f s’annulant en a.
7/ Intégration : Calcul d’une intégrale à l’aide d’une primitive
Théorème :
Soit f fonction continue sur un intervalle I deet soit F une primitive de f sur I. Alors, quels que soient a et b appartenant à I :
Le nombre F (b) - F (a) est noté avec des crochets :

Démonstration :
Notons G la fonction définie sur I par :
D’après le théorème précédent G est la primitive de f qui s’annule en a.
Deux primitives diffèrent seulement d’une constante donc, il existe k réel tel que :
pour tout x de I : F(x) = G(x) + k
Exemple :
Attention : Sur des calculs d'intégrales plus compliqués, beaucoup d'erreurs proviennent d'unemauvaise gestion du signe "-". Il faut donc faire des étapes de calcul, toujours mettre des paranthèses et bien distribuer le signe à tous les termes.
Remarques pratiques :
1)
Donc :
Faire sortir la constante permet d’alléger les calculs.
2) intégrale d’une fonction constante :
Donc, pour toute constante k :
.png)
8/ Intégration : Propriétés algébriques de l’intégrale
Propriétés de linéarité :
soient f et g fonctions continues sur l’intervalle [ a ; b ]
L’intégrale de la somme est égale à la somme des intégrales.
Pour toute constante réelle k :
Conséquence des deux propriétés : l’intégrale de la différence est égale à la différence des intégrales.
Relation de Chasles :
soit f continue sur un intervalle I et soient a, b et c éléments de I.
Remarques :
1) c peut ne pas appartenir à l’intervalle [ a ; b ].
2) Mais dans le cas où il est dans l’intervalle [ a ; b ], ce résultat se comprend aisément du point de vue des aires.
3) La démonstration de cette relation sera faite dans l’exercice n° 2.
Conséquence :
si f est une fonction continue sur [ a ; b ] :
En effet d’après Chasles :
= 0 d'où le résultat
Sommaires
Vous avez choisi le créneau suivant :
Nous sommes désolés, mais la plage horaire choisie n'est plus disponible.
Nous vous invitons à choisir un autre créneau.