Cours maths seconde

Fonctions affines

Identifier l’ensemble de définition pour une fonction définie par une courbe, un tableau de données ou une formule.La perception sur un graphique de symétries pourra conduire à une formulation analytique de ces propriétés.Retrouver l’expression d’une fonction affine à partir de sa représentation graphique.

Définitions :

Une fonction f définie sur est une fonction affine si elle peut s’écrire sous la forme f(x) = ax + b avec a et b réels.

Exemples :

   sont des fonction affines

   ne sont pas des fonctions affines

Cas particuliers

Il y a deux cas particuliers importants de fonctions affines : f(x) = ax + b

● Si b = 0, c’est-à-dire, f(x) = ax ; alors f est appelée fonction linéaire.

● Si a = 0, c’est-à-dire, f(x) = b ; alors f est une fonction constante.

● Si a = 0, c’est-à-dire, f(x) = b ; alors f est une fonction constante.

Exemples :

   sont des fonctions linéaires (et affines)

          sont des fonctions constantes (et affines)

Représentation graphique

Une fonction affine est représentée graphiquement par une droite qui n’est pas parallèle à l’axe des ordonnées.

Cas particuliers :

● Si b = 0, f(x) = ax, f est une fonction linéaire et la représentation graphique est une droite passant par l’origine O.

● Si a = 0, f(x) = b, f est constante et la droite est parallèle à l’axe des abscisses.

Exemples :

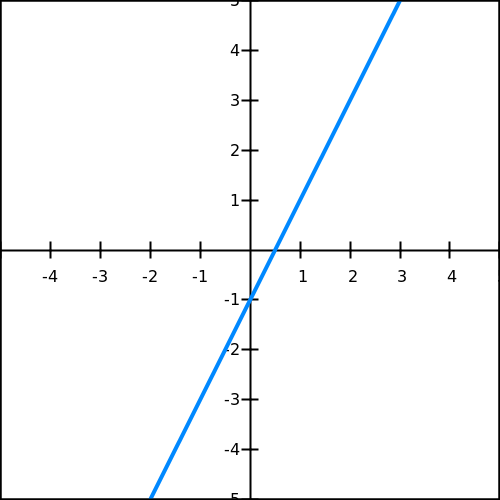
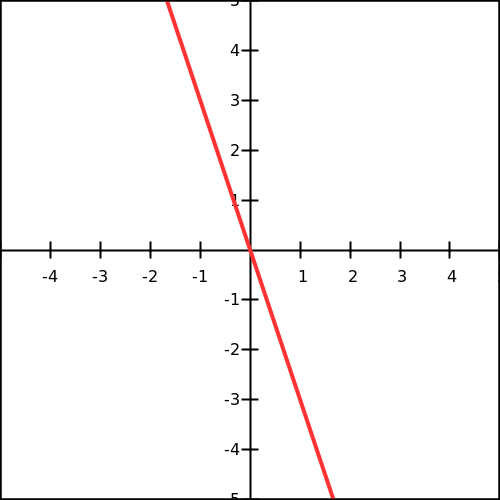
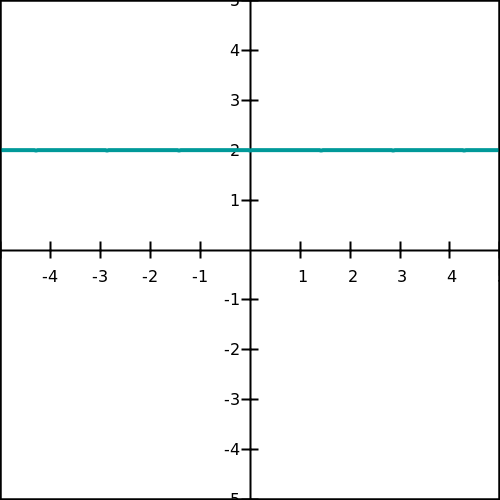
Définitions

Pour une fonction affine f(x) = ax + b dont D est la droite représentant f alors:
⇒ a est appelé coefficient directeur de D
⇒ b est appelé ordonnée à l’origine

Exemples :

f(x) = 5x- 3

Le coefficient directeur est 5 et l’ordonnée à l’origine est -3

f(x) = 1 - 2x

Le coefficient directeur est -2 et l’ordonnée à l’origine est 1

Trouver une équation de droite à partir du graphique

Méthode n°1 pour trouver une équation de droite à partir de sa représentation graphique.

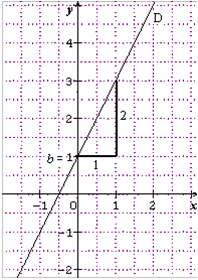
• Lecture du coefficient directeur :

Lorsque x augmente de 1, y augmente de 2
donc le coefficient directeur de D est 2 : a = 2

• Lecture de l’ordonnée à l’origine :

La droite D coupe l’axe des ordonnées au
point d’ordonnée 1. L’ordonnée à l’origine
est donc 1 : b = 1

• Conclusion :

On a donc : f(x) = 2x+ 1

 

Méthode n°2 pour trouver une équation de droite à partir de sa représentation graphique.

La droite passe par les points A(1;1) et B(4;3).

• Calcul du coefficient directeur

Il se calcule grâce à la formule :

 

 

• Calcul de l’ordonnée à l’origine

On le calcule en utilisant les coordonnées du
point A qui vérifie l’équation :

 • Conclusion

 

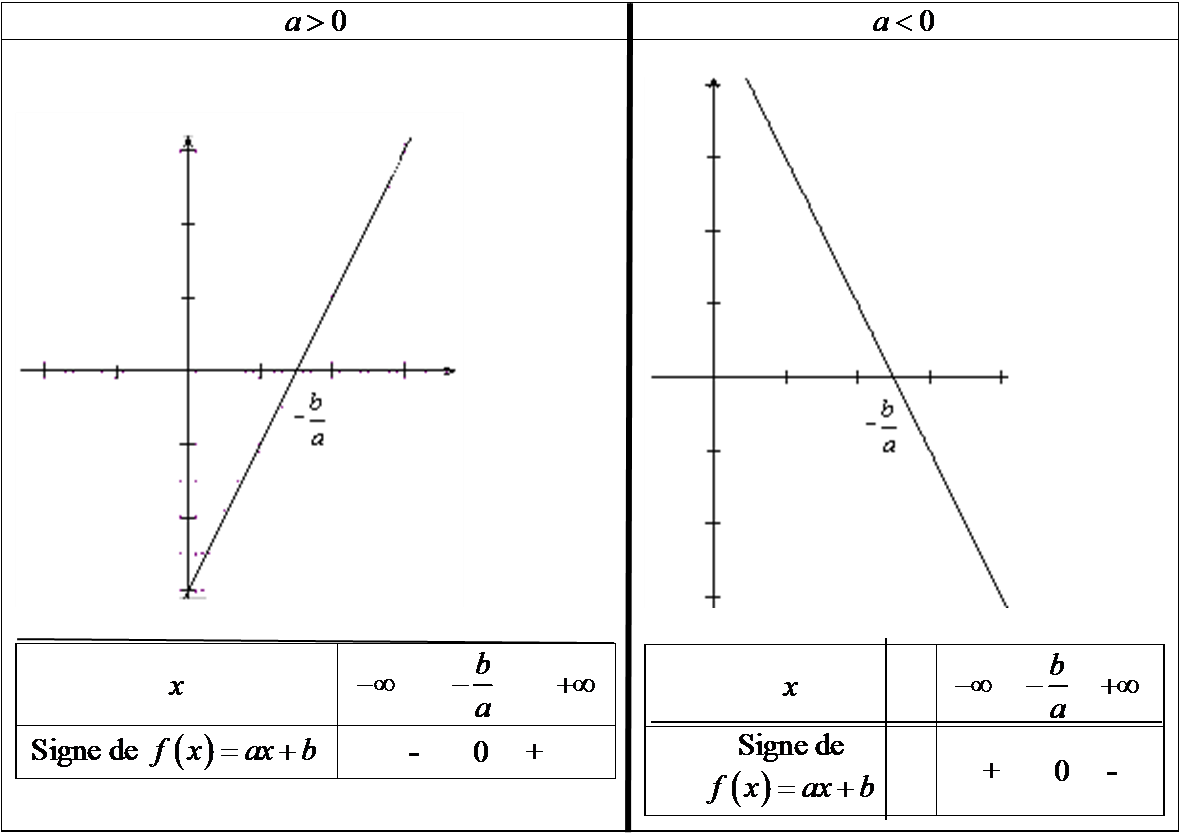
Sens de variation

Si a > 0 alors f est strictement croissante sur.

Si a < 0 alors f est strictement décroissante sur .

Si a = 0 alors f est une fonction constante sur .

Exemples :

Illustration :

Signe d’une fonction affine

Le signe de la fonction affine f(x) = ax + b dépend du signe du coefficient directeur a.

Caractérisation d’une fonction affine

Une fonction f est une fonction affine si, et seulement si, l’accroissementde l’image est proportionnel à l’accroissementde la variable. Autrement dit, x₁ et x₂ étant deux nombres réels distincts :

Méthode pour déterminer une fonction affine f connaissant sa valeur en deux points distincts :

(On connaît la valeur des images f(x₁) et f(x₂) d’une fonction affine pour deux valeurs distinctes x₁ et x₂ et on veut trouver l’expression de f(x) pour x quelconque.)

Descriptif de la méthode

1. Sachant que f est affine, on peut l’écrire sous la forme :

2. On détermine la valeur de a en utilisant la formule :

3. On détermine b en résolvant l’une des deux équations :

Exemple :

Déterminer la fonction affine f vérifiant:

 

CONCLUSION :