Cours de maths à partir de 9.90 €/heure
Cours maths 6ème
Aires - découpage et assemblage
On introduit les notions de surface d’une figure et d’aire d’une surface ainsi que les différentes unités d’aire et on effectue des changements d’unités. On met en évidence les propriétés de découpage et d’assemblage des aires. Ces propriétés sont utilisées pour comparer ou encadrer des aires.
Définitions d'une aire
Définition 1 : La surface d’une figure est la partie qui se trouve à l’intérieur de la figure.
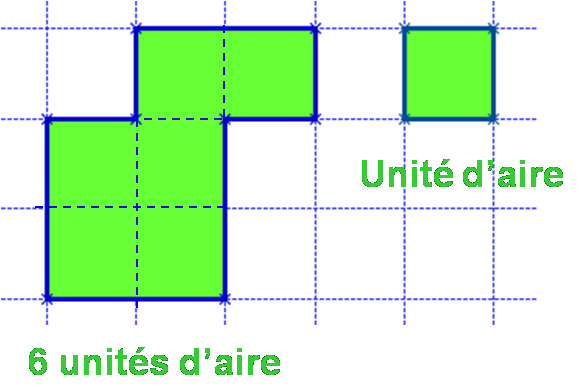
Si l’aire d’un carré est choisie comme unité d’aire, l’aire de la surface verte est égale à 6 unités d’aire.
Définition 2 : L’aire d’une surface est sa mesure dans une unité d’aire donnée.
Unités d’aire
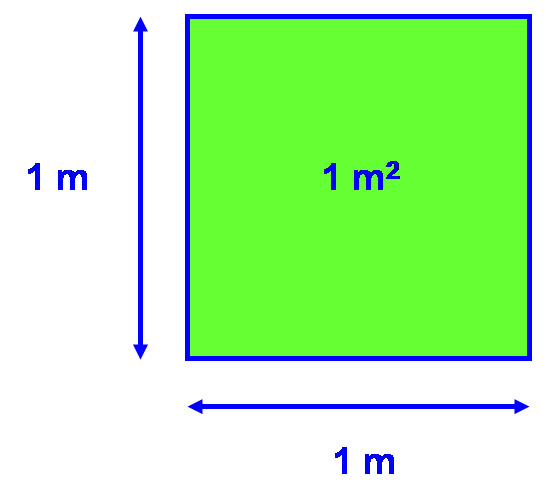
L’unité d’aire est le mètre carré, noté m2.
1 m2 représente l’aire d’un carré de 1 mètre de côté.
On utilise également les multiples et les sous-multiples du mètre carré.
Les multiples et sous-multiples du mètre carré
Les multiples du mètre carré :
Le décamètre carré : 1 dam2 est l’aire d’un carré de 1 dam de côté.
Le centimètre carré : 1 cm2 l’aire d’un carré de 1 cm2 de côté.
Le millimètre carré : 1 mm2 est l’aire d’un carré de 1 mm2 de côté.
Les unités agraires
Il existe également des unités d’aire agraires
(c’est-à-dire relatives aux terrains, aux champs, aux bois,…)
1 are : 1 a = 1 dam2
1 hectare : 1 ha = 1 hm2
1 centiare : 1 ca = 1 m2
.jpg)
Changement d’unité
Lorsque l’on passe d’une unité d’aire à l’unité immédiatement inférieure (par exemple, de m2 à des dm2), la mesure de l’aire d’une surface est multipliée par 100.
.png)
.png)
Exemple :
3,8 m2 = 3,8 x 100 dm2 = 380 dm2
Lorsque l’on passe d’une unité d’aire à l’unité immédiatement supérieure (par exemple, de m2 à des dam2), la mesure de l’aire d’une surface est divisée par 100.
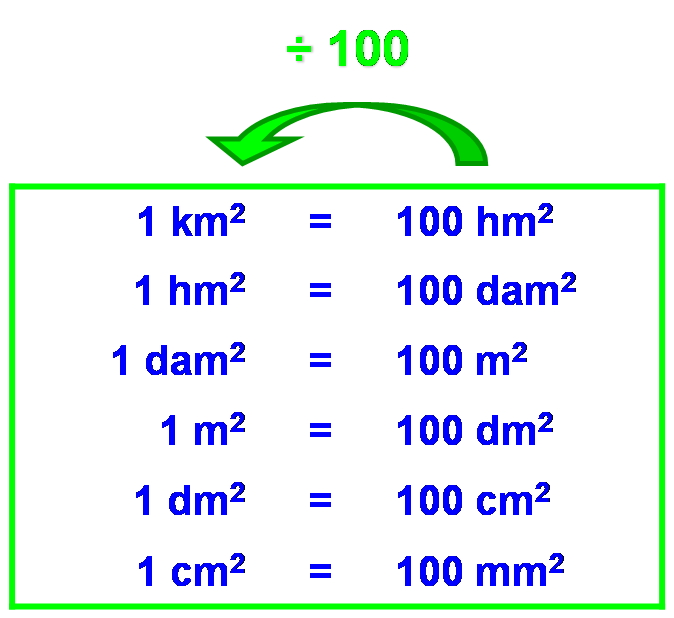
Exemple :
25 mm2 = 25 : 100 cm2 = 0,25 cm2
On a donc :
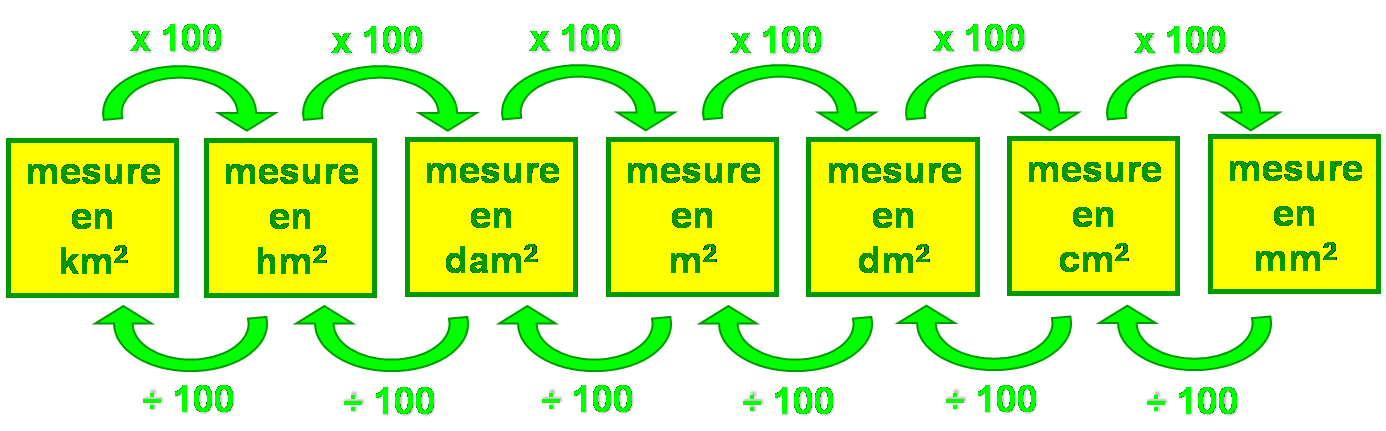
Il peut être commode d’utiliser un tableau, mais attention, il faut prévoir deux chiffres par unité.
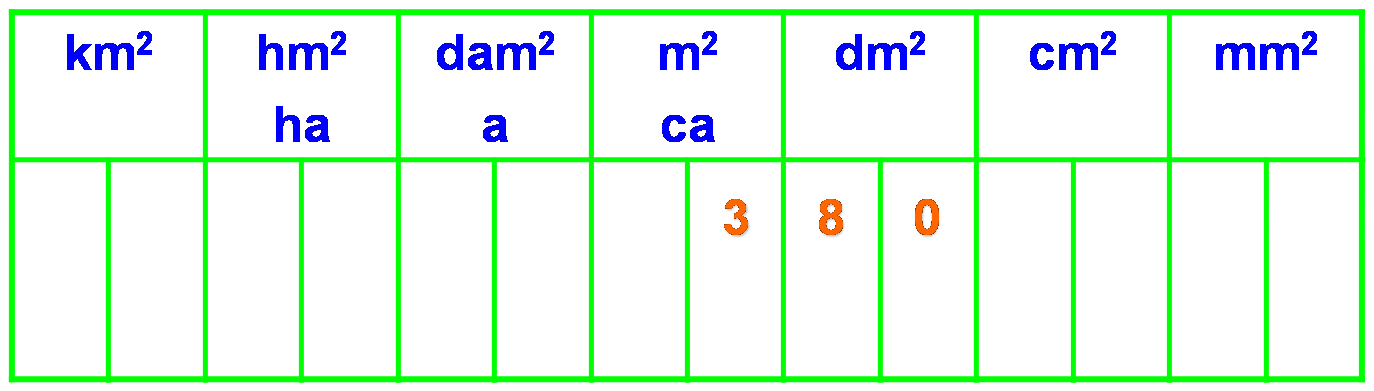
Exemple :
3,8 m2 = 380 dm2
Découpage et assemblage
Comparons l’aire des deux surfaces ci-dessous :
.png)
.png)
Si l’on compte les carreaux, on s’aperçoit que les deux surfaces S1 et S2 ont la même aire :
⇒ 10 unités d’aire
Comparons l’aire des deux surfaces ci-dessous :
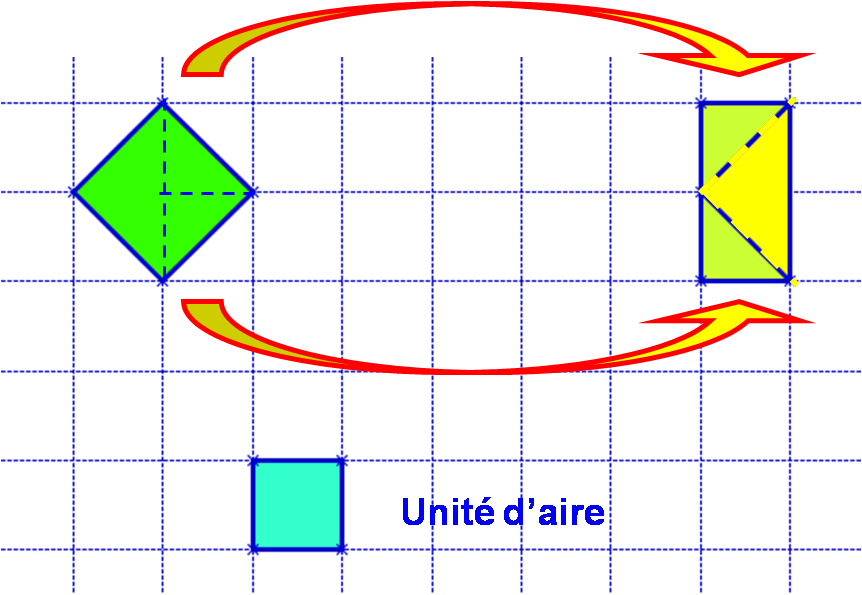
Les deux surfaces ont la même aire.
⇒ L’aire du carré vert est égale à deux unités d’aire.
L’aire d’une surface décomposée en plusieurs surfaces est égale à la somme des aires de ces surfaces.
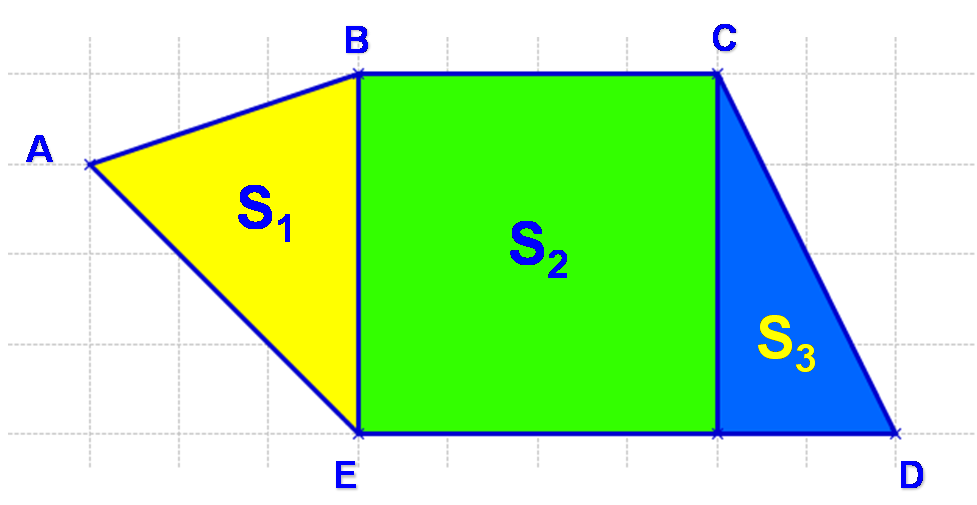
L’aire du polygone ABCDE est égale à la somme des aires de S1, S2 et S3.
Encadrement de l’aire d’une figure
Essayons de donner un encadrement de l’aire du disque ci-dessous. Pour celà, comptons tous les carrés qui se trouvent entièrement à l’intérieur, puis tous les carrés qui recouvrent entièrement le disque ...
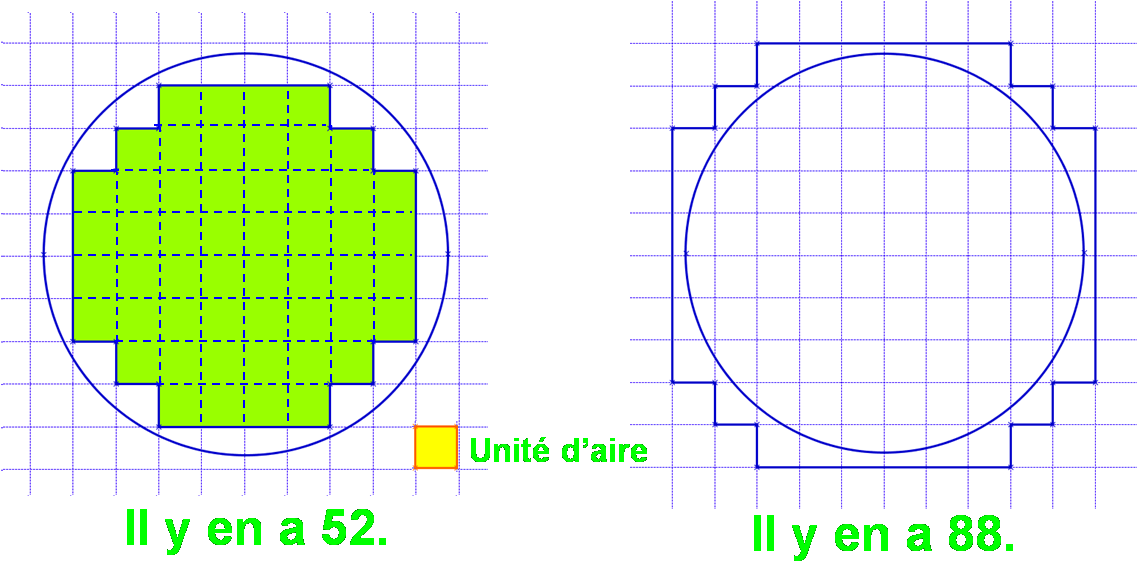
L’aire du disque est donc comprise entre 52 et 88 unités d’aire.

Sommaires
Vous avez choisi le créneau suivant :
Nous sommes désolés, mais la plage horaire choisie n'est plus disponible.
Nous vous invitons à choisir un autre créneau.