Cours maths 4ème

Distance d'un point à une droite

Il s’agit dans ce cours d’aborder la notion de distance d’un point par rapport à une droite, celle de bissectrice d’un angle et celle de tangente d’un cercle en un point. Dans ce cours, l’élève devra donc « jongler » avec plusieurs définitions et propriétés nouvelles. Il sera donc important pour l’élève de faire preuve de rigueur dans ses observations puis dans ses raisonnements.

 

Introduction à la distance d'un point à une droite

A, B, C, D et E sont cinq points distincts alignés dans cet ordre sur une droite (d). M est un point n’appartenant pas à la droite (d), tel que (MC) est perpendiculaire à (d).

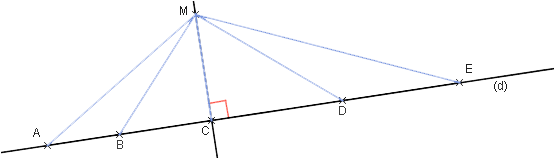
Parmi les distances MA, MB, MC, MD et ME, quelle est la plus courte ?

Le triangle MAC est un triangle rectangle en C. [MA] étant l’hypoténuse, on peut affirmer que : MC

De même :

•   le triangle MBC est un triangle rectangle en C, donc : MC
•   le triangle MDC est un triangle rectangle en C, donc : MC
•   le triangle MEC est un triangle rectangle en C, donc : MC

Conclusion :
MC est la distance la plus courte.

 

Définition de la distance d'un point à une droite

On appelle la distance du point M à la droite (AB) la plus courte distance du point M à un point de la droite (AB).

Par conséquence:

Le point de la droite (AB) le plus proche de M est le point H tel que :
la droite (MH) est perpendiculaire à la droite (AB).
Ainsi, la distance MH est, par définition, la distance du point M à la droite (AB).

Caractérisation de la bissectrice

La bissectrice d’un angle est l’ensemble de tous les points qui sont situés à égale distance des deux côtés de l’angle.

(AD) est la bissectrice de l’angle on a :

Si on prend un point quelconque M appartenant à cette bissectrice, alors on s’aperçoit que les distances qui séparent M au côté [AB) et au côté [AC) sont égales. (Dans la figure ci-dessus on a : ME = MF)

Réciproquement:

Si on prend un point situé à égale distance des côtés [AB) et [AC), alors l se situe sur la bissectrice (AD) de l’angle

Tangente d'un cercle en un point

Soient un cercle de centre O et A un point de ce cercle.

La tangente à ce cercle au point A est la droite perpendiculaire à [AO] qui passe par A

Cercle inscrit dans un triangle

1) Tracer un triangle quelconque ABC.

2) Tracer les bissectrices des trois angles de ce triangle.

3) Nous remarquons que ces trois bissectrices sont concourantes en un point noté O.

4) Tracer les trois droites perpendiculaires aux côtés du triangle et passant par O.

Elles coupent les trois côtés en M, K et L.

Que peut-on dire du cercle de centre O et de rayon [OM] ?

O étant le point d’intersection des bissectrices, OM = OK = OL. Donc ce cercle passe aussi par les points K et L. On dit que ce cercle est le cercle inscrit dans le triangle ABC. De plus, les côtés du triangle sont tangents à ce cercle en M, K et L.