Cours maths 5ème

Droites particulières d'un triangle

Dans un premier temps, la définition des médiatrices d’un triangle et la construction du cercle circonscrit à ce triangle seront étudiées. La notion de hauteur d’un triangle et celle de médiane sera vu en fin de chapitre.

Médiatrice d’un segment : définition

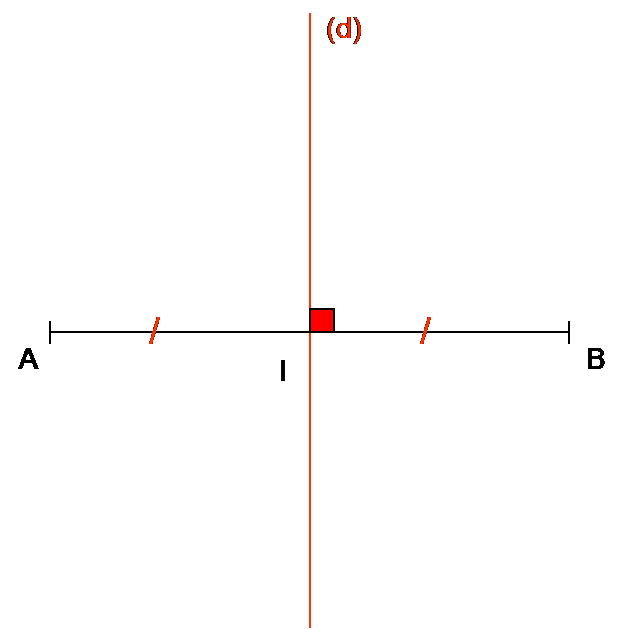Voici un segment [AB] et I son milieu.

La médiatrice d’un segment est la droite perpendiculaire au segment en son milieu.

 

Médiatrice d’un segment : propriétés

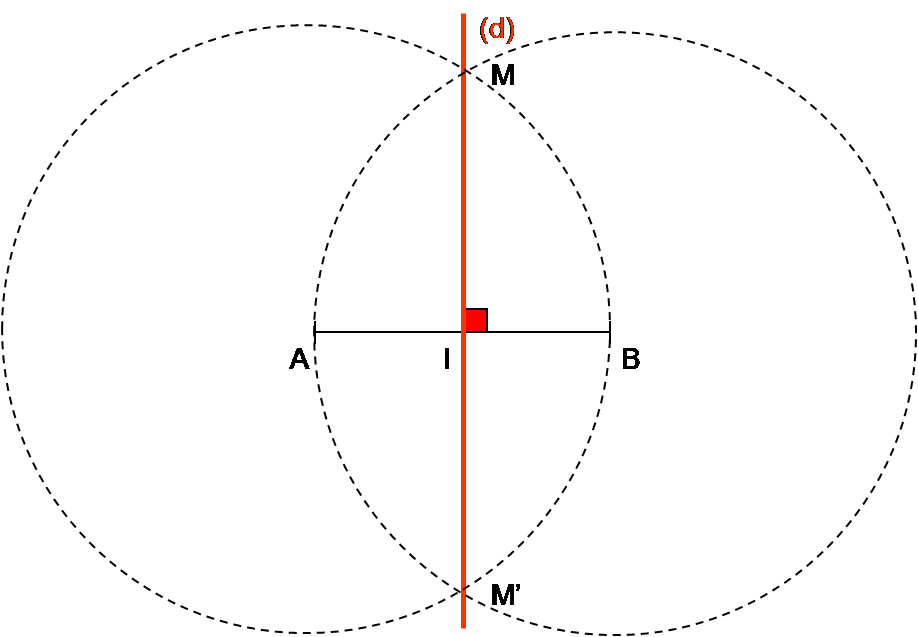Voici un segment [AB], I son milieu et (d) sa médiatrice.

On trace les cercles de centres respectifs A et B de même rayon AB.

Les deux cercles se coupent sur (d) en M et M’.

On a alors :
AM = BM et AM’ = BM’

 

Voici un segment [AB], I son milieu et (d) sa médiatrice.

Tout point de la médiatrice d’un segment est à égale distance des extrémités du segment.

Tout point à égale distance des extrémités d’un segment est un point de la médiatrice de ce segment.

 

Médiatrices des côtés d’un triangle

 

Cercle circonscrit à un triangle

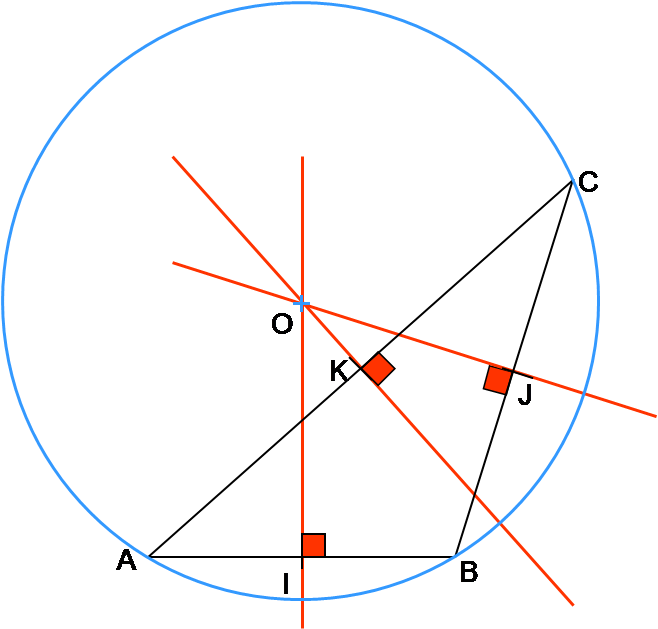O étant le point de concours des 3 médiatrices, on a :
OA = OB = OC

Les points A, B et C sont à la même distance du point O.

Les points A, B et C sont donc situés sur le cercle de centre O et de rayon OA.

 

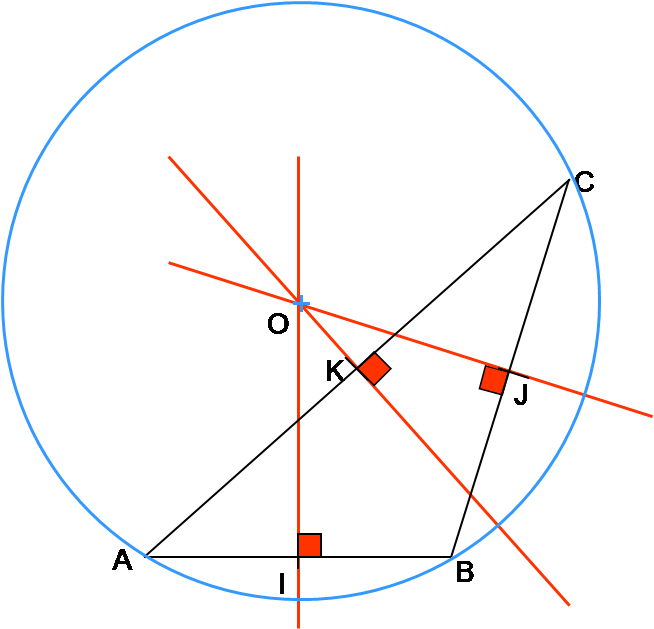Le cercle qui passe par les 3 sommets d’un triangle est le « cercle circonscrit » au triangle.

Le cercle circonscrit à un triangle a pour centre le point de concours des médiatrices du triangle.

 

Médianes d’un triangle : définition

ABC est un triangle quelconque.
I, J et K sont les milieux respectifs des côtés [AB], [BC] et [AC].

Une médiane, dans un triangle, est une droite passant par un sommet et le milieu du côté opposé.

Dans un triangle, il y a donc 3 médianes.

On admettra que les 3 médianes sont concourantes.

 

Hauteurs d’un triangle : définition

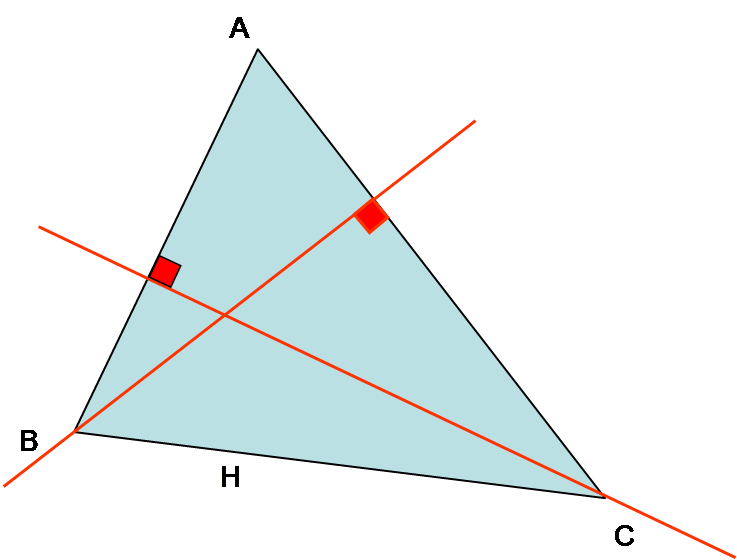ABC est un triangle quelconque.

Une hauteur, dans un triangle, est une droite passant par un sommet et perpendiculaire au côté opposé.

(AH) est la hauteur du triangle issue du sommet A.

On appellera aussi hauteur, selon le contexte, le segment [AH] ou la longueur AH.

Dans un triangle, il y a donc 3 hauteurs.

On admettra que les 3 hauteurs sont concourantes.

 

Hauteurs d’un triangle rectangle

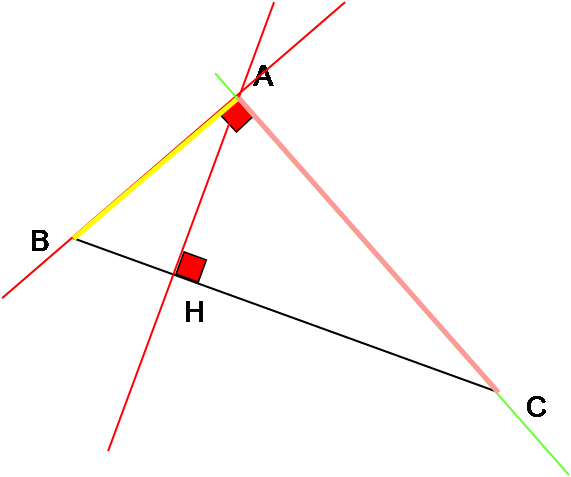ABC est un triangle rectangle en A.
On trace la hauteur (AH) relative au côté [BC].

Quelle est la perpendiculaire au côté [AC] passant par B ?
......C’est la droite (BA).

Quelle est la hauteur relative au côté [AC] ?
......C’est le côté [BA].

Quelle est la perpendiculaire au côté [AB] passant par C ?
......C’est la droite (CA).

Quelle est la hauteur relative au côté [AB] ?
......C’est le côté [CA].

Dans un triangle rectangle, les côtés de l’angle droit sont aussi hauteurs du triangle.

 

Hauteurs et aire d’un triangle

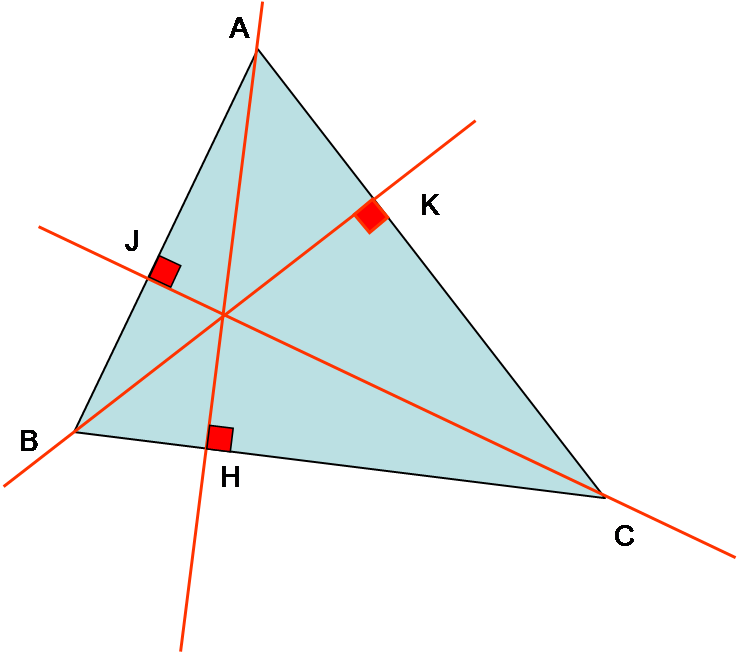ABC est un triangle quelconque.

L’aire du triangle est égale au demi produit de la longueur d’un côté par la hauteur relative à ce côté.

L’aire du triangle ABC est égale à :

0,5 x AB x CJ
ou
0,5 x AC x BK
ou
0,5 x BC x AH

Dans un triangle rectangle, les côtés de l’angle droit sont aussi hauteurs du triangle.

 

Aire d’un triangle et médiane

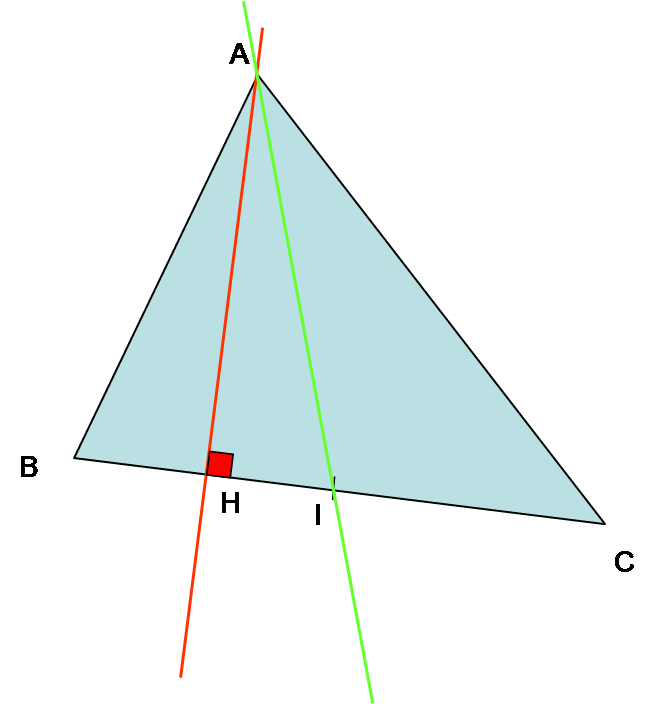ABC est un triangle quelconque.

I est le milieu du côté [BC].
(AI) est la médiane relative au côté [BC].

On appelle (AH) la hauteur relative au côté [BC]

Pour le triangle ABI :
La hauteur relative au côté [BI] est (AH).
Son aire est donc : ( BI x AH ) / 2

Pour le triangle AIC :
La hauteur relative au côté [IC] est (AH).
Son aire est donc : ( IC x AH ) / 2

 

 

ABC est un triangle quelconque. I est le milieu du côté [BC].

Le triangle ABI a pour aire :
( BI x AH ) / 2
Le triangle AIC a pour aire :
( IC x AH ) / 2

Comme I est le milieu de [BC] :
BI = IC

Les triangles ABI et AIC ont donc la même aire.

 

Propriété des médianes d’un triangle

Chacune des médianes d’un triangle le partage en deux triangles de même aire.

ABC est un triangle quelconque. I, J et K sont les milieux respectifs des côtés [AB], [BC] et [AC].

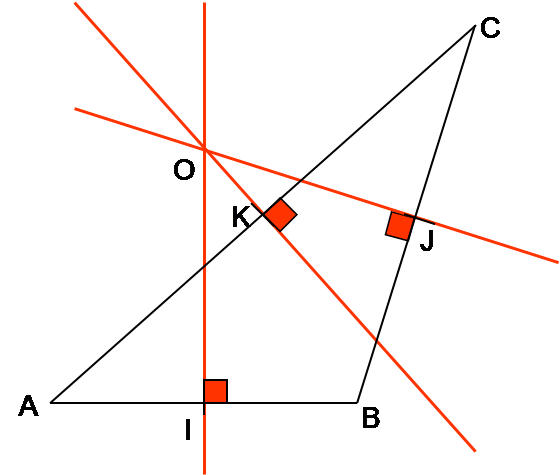
On va placer les médiatrices des segments [AB] et [BC]
Ces deux médiatrices se coupent en O.

On trace alors la médiatrice de [AC].
La médiatrice de [AC] semble passer par O.

On a alors OA = OB et OB = OC.

Donc : OA = OC

O étant à égale distance de A et de C,

O est donc un point de la médiatrice de [AC].

 

 

Dans un triangle, les médiatrices des trois côtés se coupent au même point O.

On dit qu’elles sont concourantes en O.

O est le point de concours des 3 médiatrices.