Cours de maths à partir de 9.90 €/heure
Cours maths 3ème
Polygones réguliers
Ce cours a pour objectifs de travailler autour de la définition, la construction et les propriétés des polygones réguliers. Il est nécessaire de connaitre la notion d’angles inscrits et d’angles au centre.
Définition d'un polygone régulier
Définition :
Un polygone régulier est un polygone qui a tous ses côtés de même longueur et tous ses angles de même mesure.
Parmi les polygones suivants, lesquels sont réguliers ?
Lorsque le polygone n’est pas régulier, expliquer pourquoi.
.png)
Les polygones réguliers sont :
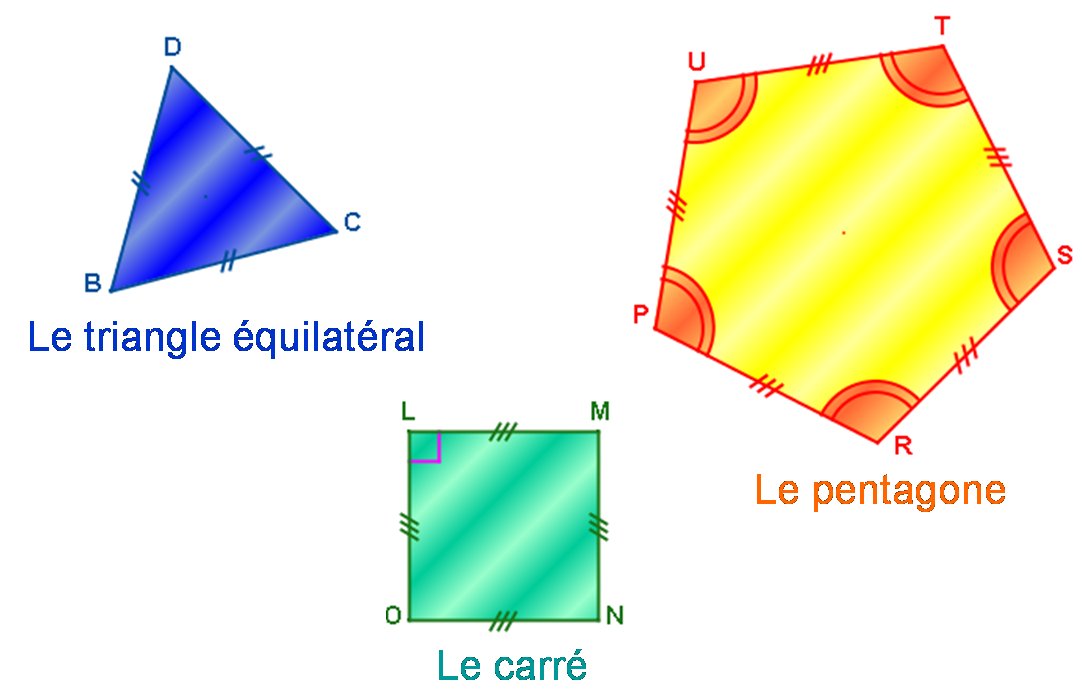
Les polygones qui ne sont pas réguliers sont :
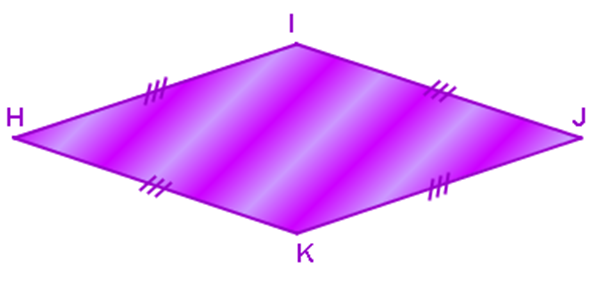
♦ Le losange :
En effet, les 4 angles du losange ne sont pas égaux.

♦ Le triangle isocèle :
En effet, le triangle isocèle n’a que 2 côtés sur 3 et 2 angles sur 3 égaux.
Polygones réguliers
Un polygone régulier est un polygone qui a tous ses côtés de même longueur et tous ses angles de même mesure.
Propriété :
Si un polygone est régulier, alors il est inscriptible dans un cercle. Le centre du cercle est appelé centre du polygone.
Activité : polygone régulier et angle au centre
Exemple :
On considère le triangle équilatéral ci-dessous. Le triangle équilatéral est un polygone régulier, il est donc inscriptible dans un cercle :
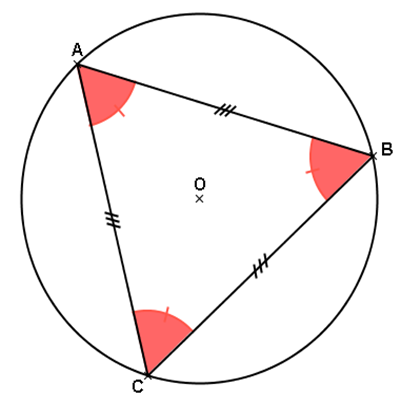
Problème : Quelle est la mesure de l’angle au centre CÔB ?

On sait que :
l’angle inscrit CÂB et l’angle au centre CÔB interceptent le même arc BC.
Or :
dans un cercle, si un angle inscrit et un angle au centre interceptent le même arc, alors la mesure de l’angle au centre est le double de celle de l’angle inscrit.
Donc :
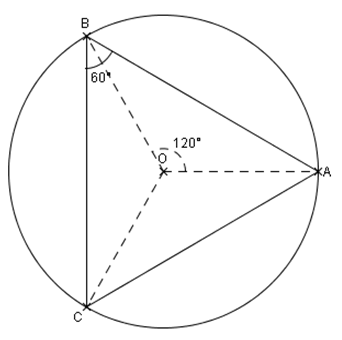
BÔC = 2×BÂC = 2 ×60 = 120°.
De la même façon, on peut démontrer que les angles au centre BÔA et AÔC mesurent aussi 120 °.
Propriété :
Si un polygone est régulier, alors la mesure de chaque angle au centre interceptant un côté du polygone est égale à :
Exemple 1 : triangle équilatéral
Pour un triangle équilatéral, les angles au centre interceptant les côtés du triangle mesurent : 360 ÷ 3 = 120°.
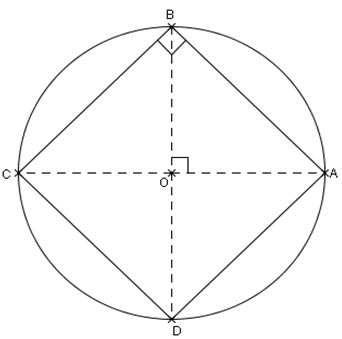
Exemple 2 : carré
Pour un carré, les angles au centre interceptant les côtés du carré mesurent : 360 ÷ 4 = 90°.
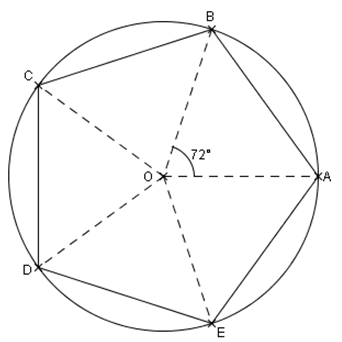
Exemple 3 : pentagone régulier
Pour un pentagone régulier, les angles au centre interceptant les côtés du pentagone mesurent : 360 ÷ 5 = 72°.
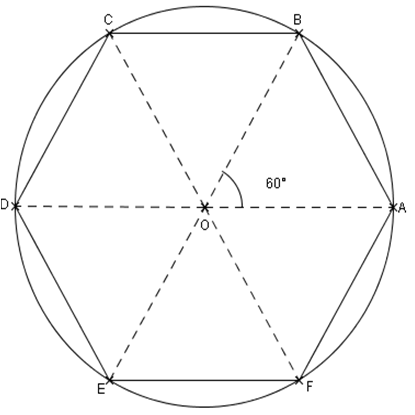
Exemple 4 : hexagone régulier
Pour un hexagone régulier, les angles au centre interceptant les côtés de l’hexagone mesurent : 360 ÷ 6 = 60°.
Sommaires
Vous avez choisi le créneau suivant :
Nous sommes désolés, mais la plage horaire choisie n'est plus disponible.
Nous vous invitons à choisir un autre créneau.