Cours de maths à partir de 9.90 €/heure
Cours maths 3ème
Sections de solides
Ce cours a pour objectifs de travailler les sections de différents solides par un plan (sections d’un pavé droit, d’un cylindre, d’un cône de révolution, d’une pyramide et d’une sphère) et les calculs de longueurs dans l’espace.
Section d’un pavé droit
La section d’un pavé droit par un plan parallèle à une face est un rectangle identique à cette face.
Exemple :
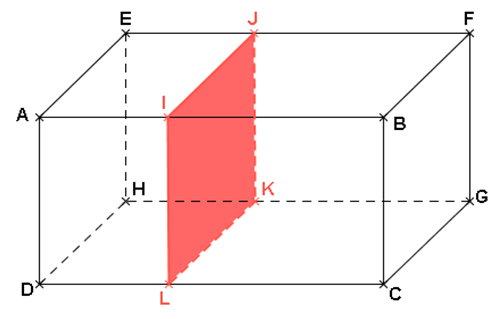
Le plan est parallèle aux faces AEHD et BFGC.
La section IJKL est donc un rectangle.
La section d’un pavé droit par un plan parallèle à une arête est un rectangle.
Exemple :
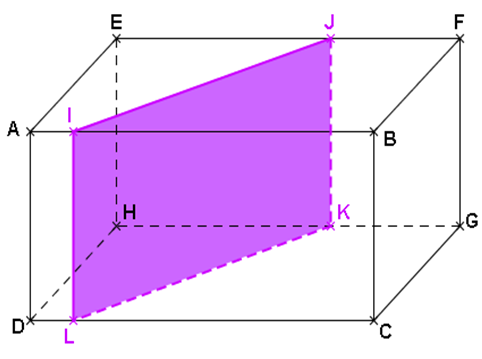
Le plan est parallèle aux arêtes [AD], [BC], [EH] et [FG].
La section IJKL est donc un rectangle.
Section d’un cylindre de révolution
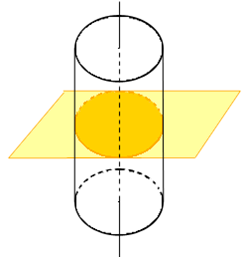
La section d’un cylindre de rayon R par un plan parallèle aux bases est un cercle de rayon R.
Exemple :
Le plan est parallèle aux arêtes [AD], [BC], [EH] et [FG].
La section IJKL est donc un rectangle.
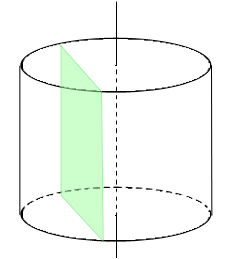
La section d’un cylindre de rayon R par un plan parallèle aux bases est un cercle de rayon R.
Exemple :
Le plan est parallèle aux arêtes [AD], [BC], [EH] et [FG].
La section IJKL est donc un rectangle.
Section d’une pyramide ou d’un cône de révolution
La section d’une pyramide ou d’un cône de révolution par un plan parallèle à la base est une réduction de la base.
Cela signifie que c’est une figure de même nature (rectangle, carré, cercle…) mais dont les longueurs sont proportionnelles à la base.
Exemple : pyramide
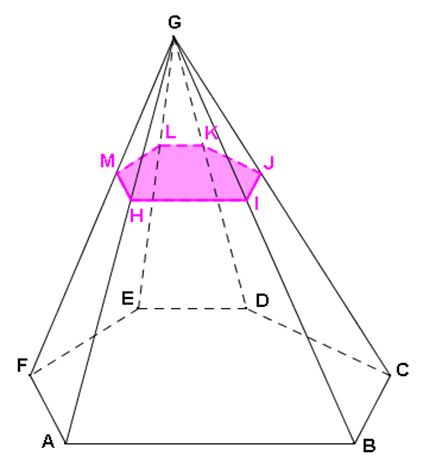
Le plan est
parallèle à la base ABCDEF.
La section
HIJKLM est donc une
réduction de l’hexagone ABCDEF.
Le coefficient de réduction est :
Exemple : Cône de révolution
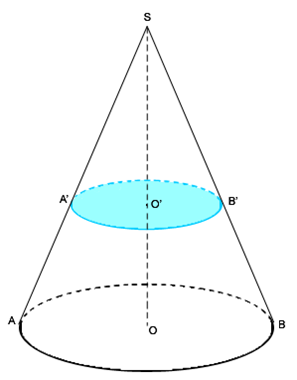
Le plan est
parallèle à la base.
La section est donc
un cercle.
Ce cercle est une
réduction de la base du cône.
Le coefficient de réduction est :
Propriétés
Quand on agrandit (ou réduit) une figure, si les dimensions
(ou longueurs) sont multipliées par k, alors :
- Les aires sont multipliées par k²
- Les volumes sont multipliés par k3.
Section d’une sphère par un plan
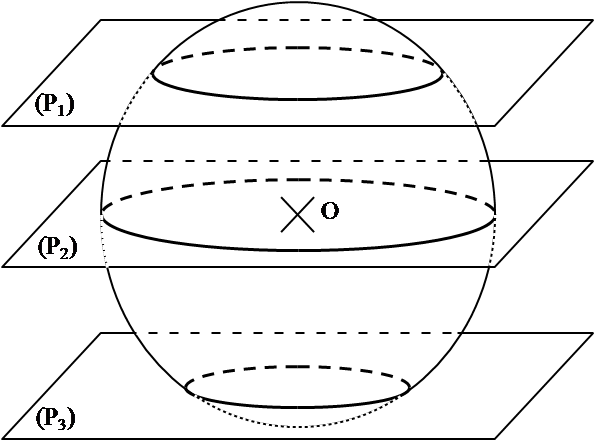
La section d’une sphère par un plan est un cercle.
Remarque :
Quand le plan passe par le centre O (Plan P2), le cercle a le même rayon que la sphère : c’est un grand cercle de la sphère.
Cas particulier : pas de point d’intersection
Si la distance entre le centre de la sphère et le plan est supérieure au rayon de la sphère, alors la sphère et le plan n’ont pas de point d’intersection.
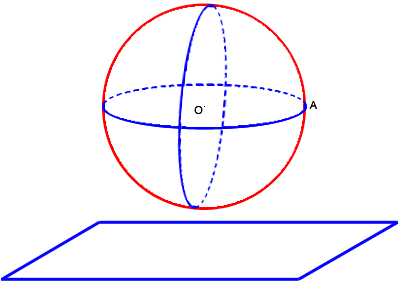
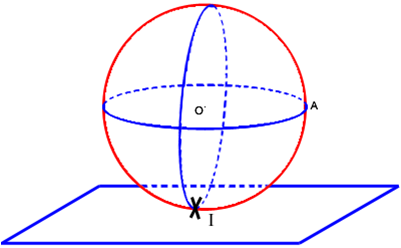
Cas particulier : un seul point d’intersection
Si la distance entre le centre de la sphère et le plan est égale au rayon de la sphère, alors la sphère et le plan ont un seul point d’intersection.
Sommaires
Vous avez choisi le créneau suivant :
Nous sommes désolés, mais la plage horaire choisie n'est plus disponible.
Nous vous invitons à choisir un autre créneau.