Cours maths 5ème

Statistiques - effectifs et fréquences

A partir d’une situation, ce cours dégage les notions d’effectifs et de fréquence ainsi que celles de classe de même amplitude. Ensuite, ce cours abordera la notion d’effectif total et de valeur de la somme de toutes les fréquences de la série statistique étudiée. Il montrera enfin, à travers une situation pratique, comment regrouper des données en classes de même amplitude.

Notes obtenues à un devoir

Voici les notes sur dix obtenues par les 26 élèves de la classe de 5A au dernier devoir :

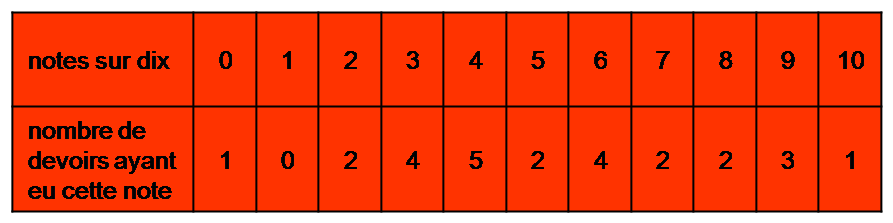
Combien de copies ont obtenu la note de 4/10 ?
5

Combien de copies ont obtenu la note de 9/10 ?
3

Quel est l’effectif de la note 0 ?
1

Quel est l’effectif de la note 6 ?
4

5 est appelé l’effectif de la note 4; 3 est l’effectif de la note 9.

Calculer la somme de tous les effectifs du tableau ci-dessus.
1 + 0 + 2 + 4 + 5 + 2 + 4 + 2 + 2 + 3 + 1 = 26

Quelle donnée de l’énoncé vient-on de retrouver ?
26 représente le nombre total d’élèves de la classe
26 représente l’effectif total

 

Effectif, effectif total

L’effectif d’une donnée dans un relevé d’observations correspond au nombre de fois qu’elle y apparaît.

L’ensemble des données du relevé d’observation est appelé souvent :
série statistique.

La somme des effectifs de toutes les observations est appelée :
l’effectif total de la série.

Notes obtenues à un devoir

L’effectif total est 26.
Calculer le quotient exact, puis arrondi au centième de l’effectif de la note 4 par l’effectif total.

5 / 26 ≈ 0,19

0,19 est appelé la fréquence de la note 5

 

Fréquence

La fréquence d’une donnée dans une série statistique correspond au quotient de l’effectif de cette donnée par l’effectif total.

La fréquence d’une donnée peut s’exprimer par un nombre décimal inférieur ou égal à 1.

La fréquence d’une donnée peut aussi s’exprimer en pourcentage.

Etude d’un tirage

Dans un sac il y a 4 boules numérotées 1 ; 2 ; 3 ; 4. On effectue 20 tirages en remettant chaque fois la boule tirée dans le sac. Les boules sont toutes identiques. On obtient le tableau suivant :

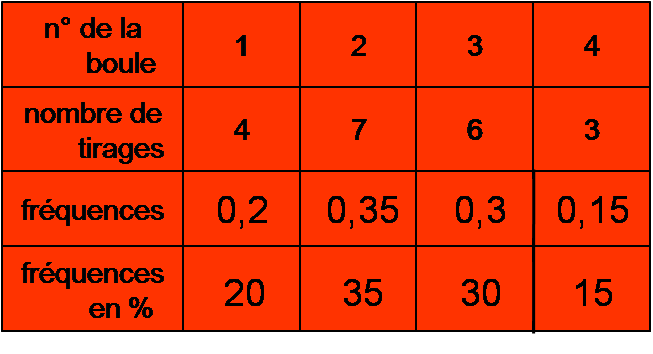
Effectif total : 20

Calculer la fréquence de toutes les observations :

 

Somme des fréquences : exemple

Calculer la somme de toutes les fréquences :
0,2 + 0,35 + 0,3 + 0,15 = 1

Calculer la somme de toutes les fréquences en pourcentages :
20 + 35 + 30 + 15 = 100

 

Somme des fréquences : propriété

La somme des fréquences des données dans une série statistique est toujours égale à 1.

La somme des fréquences en pourcentages des données dans une série statistique est toujours égale à 100.

À propos de tailles …

On a relevé la taille en cm des membres d’un groupe de 30 personnes. On a obtenu le relevé suivant :

147 ; 164 ; 158 ; 149 ; 144 ; 148 ; 156 ; 156 ; 158 ; 152 ;
151 ; 148 ; 144 ; 153 ; 158 ; 156 ; 144 ; 146 ; 159 ; 161 ;
149 ; 154 ; 147 ; 149 ; 156 ; 152 ; 153 ; 160 ; 158 ; 147 ;

On décide de regrouper ces mesures de 5 cm en 5 cm.
On va compter par exemple le nombre de tailles supérieures ou égales à 140 cm, mais inférieures à 145 cm.
Si t désigne une de ces observations, on écrira que : 140 ≤ t

140 ≤ t

On va donc pouvoir créer 5 classes et regrouper les observations dans ces 5 classes. En effet, les tailles observées vont de 144 cm à 162 cm.

Si t désigne une de ces observations, on aura les classes :

140 ≤ t 145 ≤ t 150 ≤ t 155 ≤ t 160 ≤ t

On obtiendra alors le tableau suivant :

Effectif de la classe 140 ≤ t Effectif de la classe 145 ≤ t Effectif de la classe 150 ≤ t Effectif de la classe 155 ≤ t Effectif de la classe 160 ≤ t

Regroupement en classes

Le tableau :

constitue un regroupement en classes des relevés de tailles suivantes :

147 ; 164 ; 158 ; 149 ; 144 ; 148 ; 156 ; 156 ; 158 ; 152 ;
151 ; 148 ; 144 ; 153 ; 158 ; 156 ; 144 ; 146 ; 159 ; 161 ;
149 ; 154 ; 147 ; 149 ; 156 ; 152 ; 153 ; 160 ; 158 ; 147 ;