Cours de maths à partir de 9.90 €/heure
Cours maths 6ème
Triangles
Après avoir rappelé les définitions et le vocabulaire associés au triangle, ce cours détaille les propriétés relatives aux côtés et aux angles des triangles isocèles, des triangles équilatéraux et des triangles rectangles. Ce cours montre également comment construire un triangle connaissant les longueurs de ses trois côtés.
Définition et vocabulaire
Définition Un triangle est un polygone ayant trois côtés.
Vocabulaire :
.jpg)
A, B et C sont les trois sommets du triangle
Les segments [AB] ,[AC] et [BC] sont les trois côtés du triangle
,
et
sont les trois angles du triangle
Le côté [BC] est le côté opposé au sommet A
Le côté [AC] est le côté opposé au sommet B
Le côté [AB] est le côté opposé au sommet C
Triangle isocèle
Définition : Un triangle isocèle est un triangle ayant deux côtés de même longueur.
Vocabulaire :
.jpg)
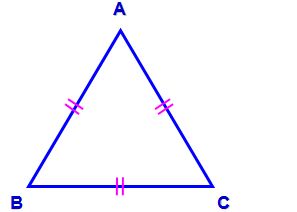
ABC est un triangle isocèle en A car
Le point A s’appelle le sommet principal.
Le coté [BC] s’appelle la base.
Propriétés :
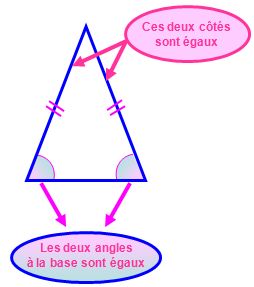
Si un triangle est isocèle alors ses deux angles à la base sont égaux.
Si un triangle a deux angles égaux, alors il est isocèle
Triangle équilatéral
Définition : Un triangle équilatéral est un triangle dont les trois côtés ont la même longueur.
Le triangle ABC est équilatéral car :
Propriété :
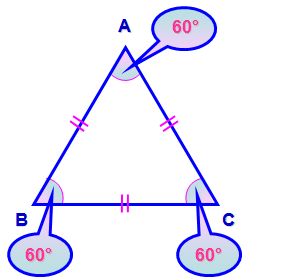
Dans un triangle équilatéral, les trois angles sont égaux et mesurent 60°.
Triangle rectangle
Définition : Un triangle rectangle est un triangle ayant deux côtés perpendiculaires.
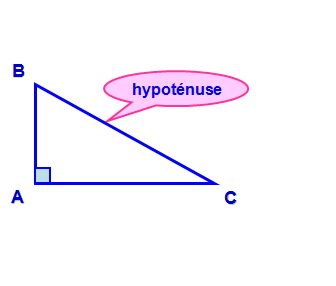
ABC est un triangle rectangle en A car
La droite (AB) est perpendiculaire à la droite (BC).
L’angle est un angle droit.
Le coté [BC] s’appelle l’hypoténuse.
Construire un triangle
Construire un triangle ABC tel que AB = 6 cm, AC = 4 cm et BC = 5 cm.
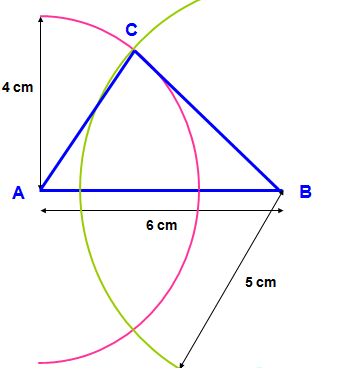
On commence par tracer un des côtés avec la règle graduée, par exemple [AB].
Comme AC = 4 cm, le point C se trouve sur le cercle de centre A et de rayon 4 cm.
De même, comme BC = 5 cm, le point C se trouve sur le cercle de centre B et de rayon 5 cm.
Le point C se trouve donc à l’intersection de ces deux cercles.
Il ne reste plus qu’à tracer les segments [AC] et [BC].
Construire un triangle ABC tel que AB = 6 cm, AC = 4 cm et BC = 5 cm.
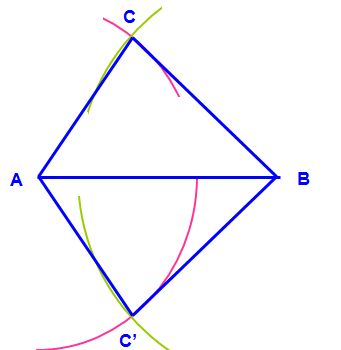
Remarque 1 :
Dans la pratique, on ne trace que
les arcs de cercle utiles.
Remarque 2 :
Le triangle ABC’ est une autre
solution
Cours complémentaires
Sommaires
Vous avez choisi le créneau suivant :
Nous sommes désolés, mais la plage horaire choisie n'est plus disponible.
Nous vous invitons à choisir un autre créneau.